PBRにおいて使われるBSDFにはエネルギー保存則の他に、相反性と呼ばれる性質が求められます。あまり日の目を浴びることはない性質ですが、物理学的に要請されるとても原則的な性質であらゆるBSDFでも満たさなくてはいけません。

この記事はそんなBSDFの相反性について、どんなことが起きるのか、一体どうやって求められたのかというのを[Veach 1997]の論文をベースに熱力学、熱輻射論と共に解説していきます。

BSDFと相反性(Reciprocity)
- エネルギー保存則
- 相反性
Helmholtzの相反性
Veachの相反性
熱力学概論
- マクロ、ミクロ
平衡状態
熱力学の法則
Detailed Balance
キルヒホッフの法則
- 熱輻射
キルヒホッフの法則の証明
相反性の証明
吸収を考慮した相反性
あとがき
QandA
参考文献

BSDFと相反性(Reciprocity)

PBRでは物体に光が当たった時、どのように反射や透過するのかをBSDF(Bidirectional Scattering Distribution Function)という統計的な関数によって表現されます。BSDFはどんな反射性質を持つかによって様々なものが考えられていますが、それらBSDFには物理学的な原則として以下の2つの性質を満たす必要があります。

エネルギー保存則

一つはエネルギー保存則というもので、反射光の総エネルギーが元の入射光のエネルギーを超えてはいけないというものです。言われたらまあ当たり前じゃんという感じではありますが、式としては以下のように積分が出てきてちょっとややこしいです。

$\displaystyle{ \int_{S^2} f(\omega_i,\omega_o) \cos{\theta_o} d \omega_o \leq 1 , \forall \omega_i }$

BSDFを設計する上ではこの性質を特に意識する必要があり、多くの場合に補正項を導入してエネルギー保存則を満たせるようにしています。なのでBSDFに謎の定数があったら多分エネルギー保存則のための補正項です。

追記、これエネルギー保存則と呼ばれていますが[Open PBR]、個人的には不適切な用語であると感じます。保存則というのは対象とする物理量が何らかの変化に対して不変であるということを表す言葉で、ここでは対象とする光のエネルギーは普通に減少する形で変化するので、これを保存則と称するのは若干ダメな気がします(あくまで個人的意見です)。(系のエネルギーが変わらないという意味で通すのであれば、式は系全てのエネルギーの保存を示唆しなければいけませんが、この式はそういうわけでもないですし微妙な感じがありますね。)とはいえ、市民権を得た用語ではあるので気にしなくてもいいと思います。

相反性

もう一つは今回の記事の主題である「相反性(Reciprocity)」というものです。ちょっとややこしい話があるので一旦BSDFではなくBRDFに着目して話を進めます。BRDFではある方向 $\omega_1, \omega_2$ に対して以下のように表される相反性を持ちます。

$\displaystyle{ f_r(\omega_1,\omega_2) = f_r(\omega_2,\omega_1) }$

BRDFに与える方向 $\omega_1, \omega_2$ が入れ替わっても、その値は変わらないということを表しています。

BRDFに与える方向を入れ替えても不変であるという所から、たまに「視点と光源を反転させても光の強さは変わらない」という説明がありますが、これは適切ではありません。

反射率はBRDFで、それが不変なんだから反射光の輝度は入れ替えに対して不変になりそうな感じはありますが、反射の輝度には入射光に対する $\cos$ 項が存在します。例えば、 $\omega_1$ 方向から輝度 $L_i$ の光を当てた時、 $\omega_2$ 方向への反射光の輝度 $L_o^{1 \rightarrow 2}$ は

$\displaystyle{ L_o^{1 \rightarrow 2} = f(\omega_1,\omega_2) L_i \cos{\theta_1} d \omega_1 }$

というように表されます( $d \omega_1$ は $\omega_1$ の微小立体角)。ここで逆に $\omega_2$ から同じ輝度の入射光を与えた場合の $\omega_1$ 方向の反射光 $\omega_o^{2 \rightarrow 1}$ は

$\displaystyle{ L_o^{2 \rightarrow 1} = f(\omega_2,\omega_1) L_i \cos{\theta_2} d \omega_2 }$

という風になります。ここで相反性を使ったとして $\omega_o^{2 \rightarrow 1}$ は

$\displaystyle{ L_o^{2 \rightarrow 1} = f(\omega_1,\omega_2) L_i \cos{\theta_2} d \omega_2 }$

となりますが、これは明らかに $L_o^{1 \rightarrow 2} \neq L_o^{2 \rightarrow 1}$ です(法線に対して対称になる時だけ投影立体角が一致するのでその時は等式が成り立ちます)。つまり、視点と光源が反転したとき、視点が受け取る輝度というのは普通に変化します。なので、正確には輝度の計算において光の順路の反転は許されません。パストレーシングでも光の経路の探索は逆順に行っていますが、輝度の計算は正しい光の順序で行う必要があるのはこれのためです。

じゃあ相反性って何の意味があるんだというような感じになりますが、これは正確に言うと「経路を反転させても入射光のエネルギー(放射束)が同じであれば、出射光のエネルギーは不変である」ということを保証するものです。もう少し平たく言えば「視点と光源を反転させても、視点に入る光のエネルギーは変わらない」ということです。先ほどの例を放射束について見てみるとわかりやすいです。

反射点の微小面積を $dA$ とすると、出射項の放射束 $d\Phi^{1 \rightarrow 2}$ は定義から次のように表されます。

$\displaystyle{ L_o^{1 \rightarrow 2} = \frac{d \Phi^{1 \rightarrow 2} }{\cos{\theta_2} d\omega_2 d A} }$

これを先ほどの式に代入すると

$\displaystyle{ d \Phi^{1 \rightarrow 2} = \cos{\theta_2} d \omega_2 dA f(\omega_1,\omega_2) L_i \cos{\theta_1} d \omega_1 }$

ということになります。反転させた場合の式は

$\displaystyle{ d \Phi^{2 \rightarrow 1} = \cos{\theta_1} d \omega_1 dA f(\omega_2,\omega_1) L_i \cos{\theta_2} d \omega_2 }$

と書くことができ、相反性を用いて整理すると

$\displaystyle{ d \Phi^{2 \rightarrow 1} = \cos{\theta_2} d\omega_2 dA f(\omega_1,\omega_2) L_i \cos{\theta_1} d \omega_1 }$

放射束 $d\Phi^{1 \rightarrow 2}$ と $d\Phi^{2 \rightarrow 1}$ について、 $d\Phi^{1 \rightarrow 2} = d\Phi^{2 \rightarrow 1}$ が成り立つことが求められました。この結果から経路の反転に対してエネルギーが不変であるということが確認できます。

BTDFについても同様の性質の表現として相反性が成り立ちますが、その形はBRDFに比べて少々形が異なります。 $\omega_1$ 側の屈折率 $\lambda_1$ と $\omega_2$ 側の屈折率 $\lambda_2$ を用いて、BTDF $f(\omega_1,\omega_2)$ の相反性は次のように定義されます。

$\displaystyle{ \frac{f_t(\omega_1,\omega_2)}{\lambda_2^2} = \frac{f_t(\omega_2,\omega_1)}{\lambda_1^2} }$

BRDFと違い屈折率 $\lambda$ が関わってくるというのが違うポイントですね。これは屈折そのものが光に対して行う幾何的な作用に由来しています。

シンプルに屈折率 $\lambda_1,\lambda_2$ の物質を合わせて、滑らかな境界面における屈折について考えてみます。ここに入射光を与えるとご存じの通りスネルの法則に沿って入射光は屈折してもう片方の物質へと入ります。

ここで問題となるのが、屈折の方向性です。屈折によって光はある程度曲げられますが、その曲げの仕方は入射光の方向に依存します。そのため、入射光は屈折によって縮められたり、あるいは広がることがあります。すなわち、入射光の立体角 $\omega_1$ と出射光の立体角 $\omega_2$ は一致しないということになります。

これによって光の密度は変化することになり、例え入射光全てが透過できたとしても単位立体角当たりの量である輝度は変化することになります。なかなかこの性質は厄介なので、屈折の幾何的作用に対して不変な輝度的な量としてBasic Radianceというものが考案されています。屈折率 $\lambda$ の媒質中の光の輝度 $L$ に対して

$\displaystyle{ Basic Radiance = \frac{L}{\lambda^2} }$

こうした屈折の事情が相反性に屈折率による調節項が含まれる理由となるわけです。追々ちゃんと証明は話しますが、BTDFも先述の相反性によって経路の反転に対して同量の入射光の放射束に対して出射光の放射束は不変であるようになります。

BRDFとBTDFの相反性をまとめると、BSDF $f(\omega_i,\omega_o)$ は $\omega_i$ 側の屈折率 $\lambda_i$ 、 $\omega_o$ 側の屈折率 $\lambda_o$ とした時、相反性

$\displaystyle{ \frac{f(\omega_i,\omega_o)}{\lambda_o^2} = \frac{f(\omega_o,\omega_i)}{\lambda_i^2} }$

が成り立ちます(わかりづらいですが、反射の場合は単純に $\lambda_i = \lambda_o$ になるのでBRDFの相反性に一致します)。

エネルギー保存の法則に対して、BSDFの相反性は(基本的に解析的なBSDFが初等関数で作られるというのもあり)あまり設計などで意識することはありません。しかしながら、BSDFの相反性はランバート BRDFであろうがMicrofacet BSDFであろうが、今後現れるあらゆるBSDFで必ず満たさなくてはいけない普遍的な性質です。

どんなでもと何ともスケールがでかい話で、一体どうやってそんなことが分かったのか不思議になります。今回の記事は背景にある物理学も含めてBSDFの相反性の証明について解説していこうと思います。

Helmholtzの相反性

恐らくPBRを学んだ方だと、先ほどのBSDFの相反性をHelmholtzの法則という名称で呼ばれているのを見たことがあると思います。この法則は1856年から1867年の間にに著名な物理学者Helmholtz先生の著書Handbuch der physiologischen Optikで取り上げられた法則です。当時はまだ光が電磁波であることを知らないぐらいの時代なので、厳密な証明とかはなかったと思いますが後年の研究者によって一般的な散乱等で成り立つ法則として厳密に証明されました。

この法則の主張は「視点と光源を反転させても視点に入るエネルギーは不変である」と、BSDFの相反性について示唆しるものです。なので一見BSDFの相反性をHelmholtzの法則と呼ぶのは正しいように思えますが、元々のHelmholtz先生の主張ではこの法則は拡散反射を考慮していないことが指摘されています[Veach 1997]。しかも証明については自明であるとして特に述べられていないとのことです。

Helmholtzの法則に対するHelmholtz先生の主張は次のようになっています([Veach 1997]より引用、著者訳 ()は著者独自の補足です)

光が任意の経路で任意の反射、屈折を受けながら点AからBまで進むとする。点Aからの最初の光線の経路に交わる平面 $a_1,a_2$ のペアを考え(これは偏光面のことを指していると思います、イメージとしては×のように交わっている2つの平面です)、同様にBに向かう光線の経路に対して交わる平面 $b_1,b_2$ のペアを考える。ここで、２つのペアの平面におけるエーテル粒子*1の振動の成分を考えてみる(当時の光の仮説なのであまり気にしなくていいです)。ここで点Aから平面 $a_1$ で偏光するある量の光 $J$ を仮定して、この光のうち平面 $b_1$ で偏光して $K$ の量で点Bに到達するとする。この時、同じ経路で光が戻った時、 $b_1$ 面で偏光するある量 $J$ の光が点Bから進む時、 $a_1$ で偏光して点Aに到達した光の量は $K$ に等しいことが証明できる。ファラデーが発見したように、屈折率に変化がなく、偏光に影響を与える磁性媒質を通らないのであれば、上記の命題は光に回数に関わらず反射、屈折、吸収、通常の分散(拡散の意味ではない)、回折など起きようとも真である。

ごちゃごちゃと難しい話をしているので要約すると、Jのエネルギーを持つ光が点Aから点Bまで行くとKまで減少する場合、逆に点BからJのエネルギーを持つ光を放ったら点Aまで行った時の光のエネルギーはKと等しくなるということを言っています。ただし、この話で仮定されているのが反射と屈折だけというとてもシンプルな場合だけです。いわゆるLambert反射といった拡散反射に関しては特については何も言っていないことがわかります。

私はHelmholtz先生の原著を見たわけではないので何とも言えませんが、[Veach 1997]の引用文を信じるのであれば確かに一般的なBSDFの相反性を示唆するものでは無いと感じます(引用部分の後にちゃんとある可能性は排除できませんが)。

とは言え、Helmholtzの相反性は後年の研究者によって「一般的な散乱についての相反性を表す法則」として拡張されているため、BSDFの相反性のことをHelmholtzの相反性と述べること自体は言葉の意味として間違ってはいないのかなとは思います(その法則にHelmholtz先生の名前を付けるべきかという問題はありますが)。

ともかくとして、あの有名なHelmholtz先生は一般的なBSDFについての相反性の証明は与えていません。今回の記事は[Veach 1997]の論文に基づいてBSDFの相反性について求めていこうと思います。

Veachの相反性

[Veach 1997]では以下の2つの法則を認めることによって証明を行っています。

熱力学平衡状態において、如何なる過程の起きる確率はその逆の過程が起こる確率と一致する(Detailed Balance)
熱力学平衡状態において、あらゆる位置におけるBasic Radianceは一定である(熱輻射のキルヒホッフの法則)

急に熱力学という単語が出てきてびっくりすると思います。今回の証明では熱力学という物理学の一分野が大きく関わってきます。「熱力学平衡状態」という用語を理解できるように、次の章では証明に必要な熱力学の話をざっと(だいぶ適当に)話していこうと思います。

Veachの証明は散乱を考える系が熱力学平衡状態という特殊な状態であると考えて議論を進めていきます。この状態はとても性質が良く、その状態における系にはDetailed Balance(もっと言えば熱力学第二法則)という原則が要請されます。これを使用すると反転に対する放射束の保存性が条件として導かれ、これを熱輻射のキルヒホッフの法則(Kirchhoff's law of thermal radiation) *2 を利用することでBSDFの相反性を求める、というような形で証明が行われます。今回の記事ではDetailed Balanceの説明(原則なので証明はないです)とキルヒホッフの法則の導出を行った上で相反性の証明を行っていこうと思います。

また、補足(?)として吸収を含めた場合の相反性についても簡単に述べておこうと思います。

熱力学概論

熱力学とはまず何ぞやという話ですが、一言でいうと「熱と物質の巨視的な性質について扱う学問」です。この章ではここで言っている「熱」と「巨視的」という用語を熱力学の簡単な歴史を踏まえて説明していこうと思います。

現在の熱力学では「熱」は「熱とは力学的エネルギーを除く高温の物質から低温の物質へ移動するエネルギーの移動形態」と定義されるものです。この説明にあるように「熱」は物質の「温度」にまつわる量であり、特に物質間でやり取りされるエネルギーの一種であるとされているわけです。高温の物質と低温の物質を接続した際、氷と水を混ぜたのを想像すればわかるようにその二つの温度は等しくなります。その際、温度を変化させる「熱」というものがやり取りされているというものです。

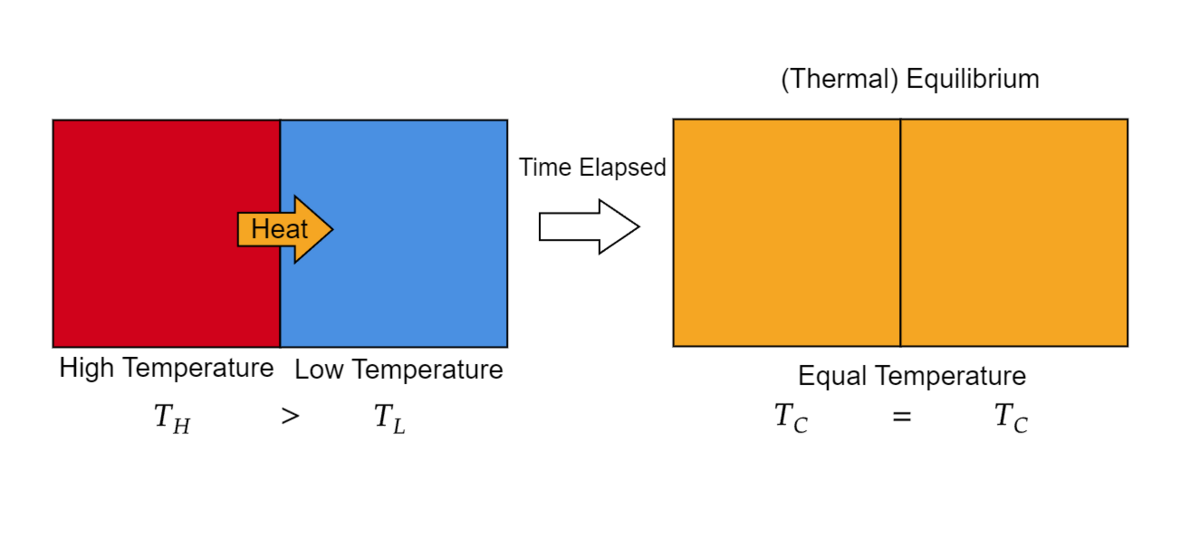
一言で言えばそういうものなのですが、この定義に至るまで非常に長い歴史があります。

熱力学の始まりははるか昔の古代ギリシャにおける「温度」の研究分野である熱学から始まっています。当時、「熱」は物質の温度を変化させる何かであり、それが物質間で出入りすることで温度が変化しているのだろうというような推測がされていました。とはいえ、温度計すらない時代でしたので熱学はまだまだ学問として体系的ではありませんでした。

熱学が体系化され始めるのは近代科学の幕開けである17世紀ごろからになります。この頃になるとついに温度計の発明によって温度の定量化がされるようになり、それに応じて熱現象に対する理解も深まり、最終的に「熱」そのものの本質について迫るようになりました。

当時の有力説の１つとして「熱はカロリック(熱素)という粒子である」と粒子的に熱を捉えるカロリック説(熱素論)が挙げられていました*3。この説によれば、物質はカロリックを持つことによって温度を持っており、それをどんどん受け取ることで温度を高めていくことができるということになります。確かにこの考え方は温度のやり取りもカロリックの受け渡しで説明できますし、直感的にわかりやすいと思います。風邪をひいたとき「熱があるね」という表現はカロリック的な表現と言えます（あとカロリー０理論とか)。

しかし、カロリック理論は摩擦熱といった力学的な運動が関わる熱現象に適用すると大きな問題点を持ちます。寒い日によく皆さんは手を擦って暖めることをすると思いますが、それは手の運動(力学的エネルギー)に由来して熱が発生させているということをしています。カロリック理論によれば、手の運動によって他の場所からカロリックを受け取ることで手が暖められていることになります。ですが、ひたすら手を擦り続けた場合、経験的に考えれば際限なく手は暖め続けられるはずです（突然効果がなくなるなんてことはないはずです)。これを満たすにはカロリックが無限にどこからか出てこなければなりませんし、供給先(この場合空気とか)は際限なく冷たくならなくてはいけなくなり、シンプルにカロリックとして考えるとおかしくなるはずです。

ということでカロリック説に対して、対称的に力学的な運動との関係性に注目して「熱は運動形態の一種である」と捉える熱の運動説が提唱されるようになりました。後年18~19世紀にかけてジュールやトムソン、クラウジウスなどの実験の結果、熱と力学的エネルギーはお互い変換することが可能であり、その変換に対してエネルギー保存則が成り立つことが確認されました。すなわち、「熱はエネルギーの一種である」ということが結論づけられたわけです。

こうして熱は力学と合流することになり、熱学から現在の熱力学が生まれることとなりました。当時は産業革命真っ盛りの中でしたから蒸気機関が与えた熱量に対してどれだけ働く(力学的エネルギー)になるのかといった実益を兼ねて熱力学は発展していきました(なので入門はやたらと熱機関の話が多い)。

このような歴史的経緯を経て、熱力学は「熱」とそれにまつわる現象を調べ、力学的エネルギー(または他のエネルギー)の関係性について導く学問として体系化されました。現在では熱力学における「温度」は物質内部のエネルギー(密度)を表す量であり、そんなわけで「熱」は

「熱とは力学的エネルギーを除く高温の物質から低温の物質へ移動するエネルギーの移動形態」

と定義されるようになりました。わざわざ力学的エネルギーを除くと言っているのは熱膨張などによって物質間で力学的エネルギーが受け渡しされるのでそれを省いているためですね(これを仕事と呼びます)。

マクロ、ミクロ

熱力学が「熱」とそれにまつわる現象を見るものであるのは何となくわかって頂けたかと思います。ですが、最初に述べた「巨視的」という表現は何なのかと思う方もいるかもしれません。この意味は「熱力学はスケールが大きい系を対象とする分野である」ということを示すものです。

また、熱力学の歴史の話に戻りますが、18~19世紀において、近代原子論の誕生に伴い、「熱」と「温度」をさらに原子レベルではどうなっているのかという研究がされるようになり、熱の運動論と合体して「熱は分子の運動エネルギーである」という説が生まれました。熱の受け渡しも分子の運動という観点からすれば、(古典的に捉えるなら)2つの物質の境界面にある分子たちが衝突するなどの相互作用を起こして、温度が低い側の分子に運動エネルギーを渡していると説明を付けることも可能です。

そうなると温度というのは突き詰めてしまえば、物質にある分子たちの運動エネルギーの何かであるということが推測することができます。マクスウェル、ボルツマンなどの活躍により、分子の力学から熱力学における物理量を接続する統計力学が誕生し、温度は分子の運動エネルギーの平均値(期待値)を表す物理量であることが理論的に示される結果となりました。

ここで言いたいことは、私たちが取り扱っていた温度というものは、物質を分子レベルまで辿ってしまえば、シンプルに分子たちの平均的な運動エネルギーを示す表現でしかないわけで、系の構成単位である分子自体は温度を持つわけではありません。すなわち、温度は分子が大量にあるような世界になって初めて現れる統計的な物理量なわけです。私たちが物質に対して考える圧力、体積など多くの物理量は分子の統計的な量です。

物理学では系を構成する粒子1つ1つを判別して考える系を微視的(ミクロ)、逆にそうした粒子を判別できないとする巨大な系を巨視的(マクロ)と表現し、特に巨視的系において初めて現れる統計的な物理量のことを巨視的であると表現します。

系の状態を完璧に知るには、本来であれば系の構成単位(分子、原子など)の運動状態を1つ1つ全て知る必要がありますが、そんなことは現実的に不可能です。しかしながら、私たちは構成単位の世界を知らずとも巨視的な物理量とそれらの関係を使うことでも、物質の状態や運動を取り扱うことができます。熱力学はそうした巨視的な量の普遍的な関係性を導いてきました。

そんなわけで、熱力学が対象とするスケールは私たちのスケールだけでなく、更に巨大な宇宙といったスケールでも成り立つような統計的で普遍的な性質について調べようというかなり(意味的にも)スケールがでかい分野でもあります(だからなんか宇宙の熱的死とかいう話が出てくるわけです)。歴史的経緯もあるので熱力学は単に熱に関わる学問と説明付けられる感じはありますが、個人的にはこれが本質的な内容だと感じます。

それでなんでPBRと熱力学が関係するのかと思うでしょうが、PBRが扱う物理量も巨視的量の一つだからです。PBRでは放射束や放射輝度という光の量を使っていますが、これは光子の集まりを表す量であり、いわば光の巨視的な量であるといえます。そう考えれば、PBRの普遍的性質を求めるのに熱力学が出てくるのは納得できるかと思います。

平衡状態

熱力学では最も重要な状態として平衡状態というものがあります。系のある巨視的物理量が時間がいくら経っても変化しなくなった時、系はその物理量に対して平衡状態にあると言います。

例えば、高い温度の物質Aと低い温度の物質Bをくっつけて長い時間放っておいた時、AからBへと熱が移動し続けて最終的にはAとBは同じ温度になった後ずっと同じ温度になり続けます(外部から何かなければ)。この時、巨視的な物理量である温度は時間に不変になるということなのでこの系は熱的に平衡状態であると言えます。

もちろん他にも2つの空気を混ぜて放っておいたら混ざって均一になるように、力学的に平衡状態にもなりますし、様々な物理量に対しても平衡状態が成り立ちます(物理量によって熱平衡、力学的平衡とか言ったりする)。

特に系の熱的、力学的、化学的な巨視的物理量が平衡状態にある時、系は熱力学的平衡状態(thermodynamic equilibrium)であると言います。

一般的に熱力学は平衡状態を考えて、平衡状態における物理量の関係について理論を考えていきます(平衡熱力学)。ちなみに非平衡状態を取り扱う熱力学は非平衡熱力学と呼びます(今回は関係ありません)。

平衡状態の重要な背景にはエネルギー輸送の不変性があります。微視的に考えれば分子というのは絶えず動いているので、平衡状態でも内部的にはエネルギーのやり取りは行われているはずです。ですが、平衡状態ではその渡すエネルギーと受け取るエネルギーの収支が釣り合うことで、巨視的に見ればエネルギーの変化は+-0となっています。従って、時間が経っても巨視的物理量は変わらないというわけです。

つまりは、平衡状態はエネルギーの輸送がどんな場所どんな方向でも収支が合うことで成り立っているわけです。これは非常に重要なことなので覚えておいてください。

熱力学の法則

熱力学では第0から第3まである基本的法則を認めて話を進めています。今回はそこまで関わらない第3法則を省いて0から2まで述べていきます。

ちょっと言い回しが難しいですが、意味自体は割と当たり前のことをしていますので、わりかし砕けた感じで説明しようと思います。

熱力学第0法則

「物質A,B,Cがあり、AとB、BとCが熱平衡である時、AとCは熱平衡である」

この表現はちょっと分かりづらいですが、ABCという３つの物質が並んでくっついている状況を考えてください。AとB、BとCが同じ温度である時、AとCは同じ温度であるということを意味しています。

これのおかげで間にいくら物質が挟まろうとも端同士の物質が同じ温度にすることが可能になります。これの嬉しさは温度計がちゃんと測りたいものの温度を最終的に示していることを保証できるというわけです。

何をそんな当たり前のことを言ってんねんという感じですが、当たり前のことを定義するのが法則なので置いておいてください。というかその感覚は正しくて、当たり前すぎて後々になって「あ、そういえば法則が足りないな」みたいなノリで追加された経緯があります(だから0という変な数字が割り振られてる)。

熱力学第1法則

熱はエネルギーの一種と言いましたので、当然これにはエネルギー保存則が成り立つ必要があり、熱が増えたなら外部からエネルギーを受け取っているということですし、逆に熱が減ったなら外部にエネルギーを渡していることになります。

ということでそれを意味する式として次のようなものが熱力学第一法則として定義されています

$\displaystyle{ \Delta U = W + Q }$

ここでの $\Delta U$ は系のエネルギーの変化量、 $W$ は系が外部に行った仕事、 $Q$ は外部から系へと移った熱量を意味します(これらは方向はどちらでもいいので負になってもOKです)。系が仕事をしたり、熱量を受け取ったりした場合は、エネルギー保存則に従ってその分だけ内部のエネルギーは変化するということを表しています。

熱力学第一法則はいくらマクロを考えていると言ってもちゃんと力学の大原則であるエネルギーは守られているということを明示しています。

熱力学第2法則

今回の話で一番重要なのがこの第二法則です。この法則は熱のやり取りのようにエネルギーの授受の方向性を述べるものなのですが、色々な人が試行錯誤した経緯があるせいかいくつか等価な表現があります。

今回はそのうち、一般的に使われている「エントロピー増大の法則」という表現を採用します。ちゃんとした説明にはエントロピーという量が必要になってきてそれこそ熱力学の記事になるのでここでは詳しく取り扱わず、だいぶ平たくした言葉で述べることにします。

「外部から断熱された系は自発的に熱力学的平衡状態へと向かうようにエネルギーの受け渡しをする。また、最終的に熱力学的平衡状態になった場合、外部からの仕事がない限りそこから自発的に変化することはない」

外部から断熱されたというのは系と外部で何らかのエネルギーのやり取りが一切ないことを意味しており、系が完全に孤立しているというを表しています。そんな状態の系は自発的、つまりは勝手に熱力学平衡状態に向かって状態を変化させることをここでは主張しています。

熱のやり取りを考えると、第二法則から低温と高温の物質2つは熱平衡状態(=同じ温度)へとならなければならないので、熱というのは自発的には高温から低温へとしか移らないということが第二法則から導かれます(というよりその事実を一般的に表現したのが第二法則)。

熱だけではなく、系のエネルギーは外部からの影響がない限り平衡状態になるような方向へと動いていき、最終的には熱力学的平衡状態へと到達します。これが第二法則で述べていることです*4。

そしてもう一つ重要な点として一度熱力学的平衡状態へとなった場合、自発的に平衡状態が崩れることは外部から影響がない限り絶対にないということを表しています。よく「氷が水に溶けたらもう自動では氷にならない」とか「混ざったものは勝手に分離しない」とか説明があると思いますが、これを一般的に表したのがこれというわけです。

この性質を先ほど述べたエネルギー輸送の話と照らし合わせれば分かりやすいです。一度平衡状態になれば当然ながらあらゆるところでエネルギーの収支が合うため、系の何かに作用するエネルギーも必ず打ち消すような逆のエネルギーが存在します。従って、平衡状態では自発的に系自身を変化させることはできないと言うことになります。

この性質はどんなエネルギー輸送でも満たさなくてはならないため、平衡状態でのエネルギーの式はあらゆるところで＝が成り立ちます。この性質は今後の証明の前提になるので覚えておいてください。

ちなみに外部からの影響があった場合はその限りではないので、何らか外部のエネルギーを受け取る、または外部にエネルギーを渡すというようなことがある場合、平衡状態を解くことが可能になります(エアコンとか冷蔵庫は外部エネルギーを使っているので一部分を冷却するなんてことが可能であるというわけです)

Detailed Balance

さらっと平衡状態のエネルギー輸送について常に収支が合うようになると述べましたが、これには重要な原理を含んでいます。エネルギーの収支がどこでもかつ、どの方向でも成り立つということはあるエネルギー輸送の過程があった時、それに対して全く反対の過程が同じぐらい起きないとそんなことは生じないわけです。ある方向にエネルギーを放てば、逆にその方向から同じ量だけエネルギーが返ってこなければ収支が合うはずがないわけですから。

そのため、平衡状態は「平衡状態のある(微視的な)過程に対して、その逆の過程が同じ確率で起きている」ことになります。これは熱だろうが力学的だろうがどんな過程においても成り立たなくてはならないため、非常に重要な原理であり、これを詳細釣り合い Detailed Balanceと呼びます。

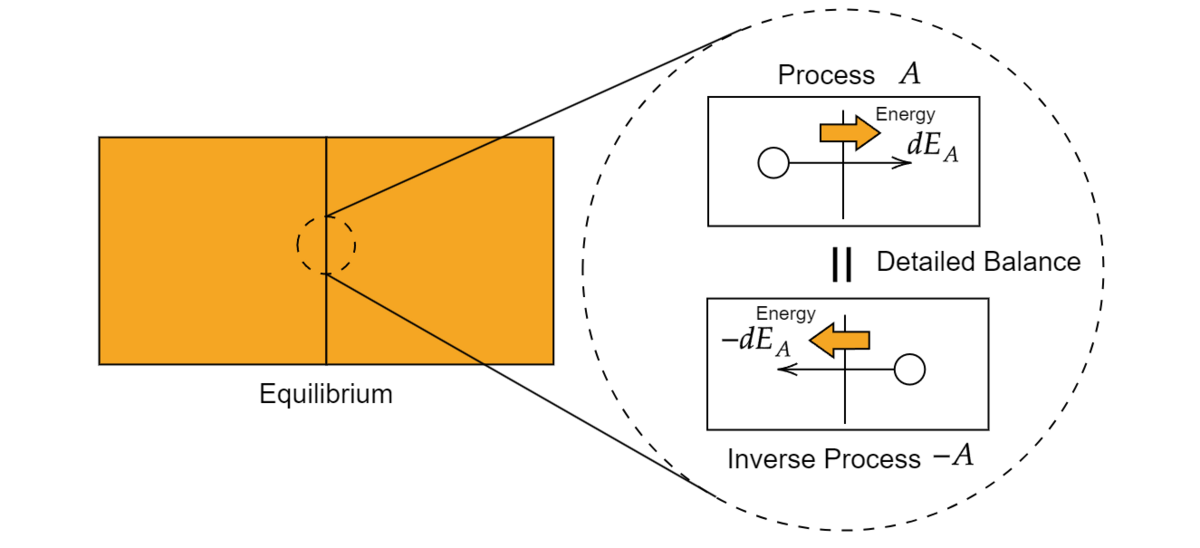
まあ何となく感覚的にわかる感じはありますが、実際あらゆる過程にその逆の過程が必ず存在し得るのかと問われるとほんとか？という感じにはなります。どんなめちゃくちゃぐにゃぐにゃした軌道を取るような粒子があったとしても、その軌道は一方向であってはいけません。全く逆の軌道を粒子が辿れることが保証される必要があります。

これについて、ありがたいことに力学の時間反転対称性と呼ばれる性質によってどんな軌道を取ろうとも、それに対して反対に辿る運動が必ず存在し得ることが保証されています。この性質はDetailed Balanceの微視的な根拠として扱われています。

時間反転対称性とは何ぞや思いますが、これは力学の基本方程式について時間 $t$ を反転させ $t \rightarrow -t$ 運動を逆回しにした時、その経路が元の時間の基本方程式を満たすという性質のことを言います。要は時間を反転させる形でで逆の軌道をちゃんと存在することを示せるというわけです。

例えば、ニュートン力学における基本方程式はポテンシャルを $V$ として、粒子の運動を $r(t)$ と表すことにすると

$\displaystyle{ m \frac{d^2 r(t)}{d^2 t} = - \nabla V(r(t)) \tag{1.1} }$

という形で表現されます。この時、 $t \rightarrow t' = -t$ に置き換え、時間を逆戻しにして今の軌道を逆方向から辿ることを考えます。この逆戻しの運動 $r(t')$ について運動方程式は

$\displaystyle{ m \frac{d^2 r(t')}{d^2 t} = - \nabla V(r(t')) }$

となります。ここで、微分の関係から

$\displaystyle{ \frac{d^2 r(t')}{d^2 t'} = \frac{d^2 r(-t)}{d^2 t} }$

ということになり、 $t' = -t$ を代入すると

$\displaystyle{ m \frac{d^2 r(-t)}{d^2 t} = - \nabla V(r(-t)) \tag{1.2} }$

と得ることができます。逆回しの運動 $r(-t)$ が満たすべき方程式は式(1.1)と見比べると全く同じであり、 $r(-t)$ は運動方程式(1.1)の解であることがわかります。つまり、逆方向に辿る経路 $r(-t)$ は元の運動方程式を満たす実現可能なものであるということが導かれます。

色々細かい話はありますが、微視的な世界であればニュートン力学や量子力学、電磁気学 *5は時間反転対称性があることが知られており、基本的にミクロな運動は可逆であることが保証されています。

まとめると、粒子がどんなに凄まじい軌道を取っても、それを逆に辿る運動が実現可能であるということを保証してくれます。なので、どんな微視的な過程もその逆となる過程が存在しており、平衡状態ではそれらが同じ確率で起きていることでエネルギーの釣り合いが取れているというわけです。

キルヒホッフの法則

長々と熱力学の話をしてきましたが、ようやく光に関する話に入っていこうと思います。

前々項で[Veach 1997]の証明の前提にキルヒホッフの法則というものがあると述べました。これは熱力学平衡状態において、媒質の屈折率 $\lambda$ とその内部の光の輝度 $L$ について、次のような量が一定であるという法則です*6。

$\displaystyle{ \frac{L}{\lambda^2} = Const. }$

これはつまり、熱力学平衡状態になると系のあらゆる場所におけるBasic Radianceは全部同じ値になるというものです。系に水があろうともガラスがあろうとも、どこを見てもBasic Radianceは完全に系で同じ値になるというわけです*7。

熱輻射

こんな法則が出るなんて不思議な話に感じるかもしれませんが、光をエネルギー輸送の一種と見なせばわかりやすいです。

一般的に私たちが見る世界だと光る物質というのは限られたものだけのように思えますが、実は物質は温度を持つだけで常に光を放出しています。こうした温度によって物質が電磁波を放つ現象のことを熱輻射、または熱放射(thermal radiation)と呼びます。この記事では参考書に従って熱輻射と呼びます。

熱輻射は物質の光学的性質の影響もありますが、一般的に温度に依存して放つ光の分布が変化します。高い温度であればあるほどより高いエネルギー(波長が短い)光を放ちやすくなり、温度が低いとエネルギーが低い光しか出せないというような性質があります。私たちが熱輻射をなかなか見ないのは1000度といった高い温度じゃないと可視光が出てこないためですね。

光はエネルギーを持つ以上、熱輻射を行うと放出した光のエネルギーの分だけ内部エネルギーを減少することになります。そうなると物質の温度というのは熱放射によって低くなっていきます(いわゆる放射冷却など)。

一方で、一般的な物質は光を当てられた時、入射光の一部のエネルギーを内部エネルギーとして吸収することが知られています。そうなると物質の温度というのは光を当てるだけで暖められていきます。輻射光を当てたとしても同様です。

つまりは温度が高い物質Aと低い物質Bを離して置いた時、Aからの輻射光によってBが暖められるというようなことが起きます。また、反射して帰ってきた光もBに当たりエネルギーを与えるというような現象が起きます。したがって、熱輻射光を含め光というのは熱の伝わり方の一つと見なすことができます。

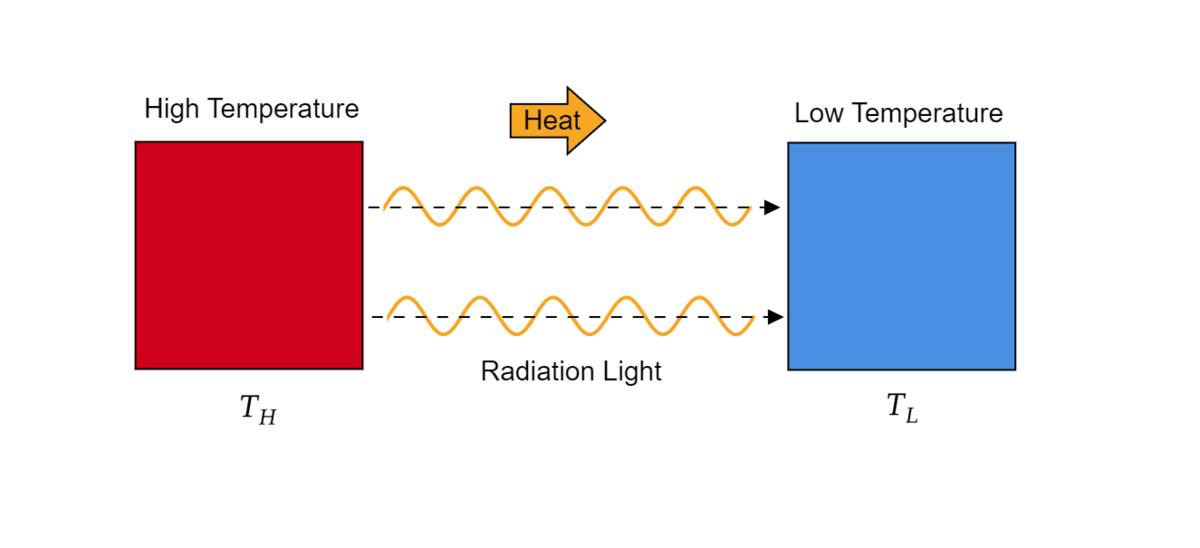
熱力学第二法則に基づけば、熱力学的平衡状態においては熱の伝わり方に偏りが生まれることは許可されていません。すなわち、平衡状態におけて熱輻射も、空間中の光にもエネルギー的な偏りが生まれることはあってはならないことです。キルヒホッフの法則が述べる「どこの位置でもBasic Radianceが等しくなる」現象は平衡時において光のエネルギーの偏りがどこにもないということを述べているに過ぎないというわけです。

キルヒホッフの法則の証明

言葉では何となくキルヒホッフの法則の意味が分かってきたと思います。ここからはちゃんと物理学的にキルヒホッフの法則について導出を行っていこうと思います。

証明の流れとしては以下のような流れで行っていきます。

(1) 無限遠に広がる一様媒質内の輝度
(2) 無限遠に広がる一様媒質内の散乱
(3) 大きさに制限がある媒質と(1),(2)の関係
(4) 異なる媒質間における輝度の関係

基本的に無限遠に広がる一様媒質での平衡状態の性質について考え、それを私たちの世界で一般的な媒質にその性質を適用して境界面の関係性を導くことで、最終的にキルヒホッフの法則を導出します。

(1)無限遠に広がった一様媒質内の輝度

証明の最初のステップとして無限遠に広がった一種類の一様媒質が平衡状態の時、その中の輝度はどうなるか考えていきます。「無限遠に広がった一様媒質」ではどの位置で合っても何らかの密度や光学的性質は変わらず、どこを見ても全く物質として同じであるというような状態です。

この媒質が平衡状態である時、物質の性質が位置に依存しないのでどこを見ようが変わらないはずです。したがって、媒質内部を行き交う光の放射輝度は方向依存性もないと考えられます。これは各波長の輝度でも同様であると考えられるので、次のようなことを要請して話を進めていきます。

媒質内の波長 $\lbrack \nu, \nu +d\nu \rbrack$ の間にある光の放射輝度 $L_{\nu}$ は方向依存性がない。

媒質の中では各領域で熱輻射による光の放出とその光の吸収という形で光が飛び交っているはずです。平衡状態である以上、どんな小さな領域 $d\tau$ でもこの放出の光エネルギー $dE_{out}$ と吸収の光エネルギー $dE_{in}$ は釣り合っていなければなりません。まずは微小体積 $d\tau$ におけるそれぞれのエネルギーを具体的に求めてみましょう。

物質がどのような輻射光を出すかは物質の種類と温度、方向など様々なものに依存しますが、今回は一様な媒質を考えているため物質の種類と温度のみに依存する定数として考えることができます。ここで、体積 $\tau$ が時間 $dt$ で立体角 $d\omega$ に放つ波長 $\nu$ の輻射光のエネルギーを輻射係数 $\epsilon_\nu$ を導入して次のように定義することとします。

$\displaystyle{ \epsilon_\nu d\nu d\omega d\tau dt \tag{3.1} }$

これについて積分していくことで輻射光全体のエネルギーについて求めることができます。 $d\tau$ はあらゆる方向に輻射光を放っているのでまず立体角全体で積分し、波長全てで積分すれば「単位体積、単位時間に放つ輻射光のエネルギー」として $d E_{out}$ を求めることができます。

$\displaystyle{ d E_{out} = d\tau dt \int_\Omega \int_0^\infty \epsilon_\nu d\nu d\omega = 4 \pi d\tau dt \int_0^\infty \epsilon_\nu d\nu \tag{3.2} }$

一方で、吸収について考えてみます。 $d\tau$ にはどの方向からも $L_\nu$ の光が来ており、 $d\tau$ はこれを吸収します。この過程だけを抜き出すため、一度 $d\tau$ を真空中に置き、半径 $r$ 球で囲んであげて同じ放射輝度 $L_\nu$ で照らしてい上げる状況を考えます(これは一様媒質で照らされている場合と等価なモデルです)。

球面の微小面積 $dA$ から放たれて $d\tau$ を通過した光についてまず考えます。任意の形状でやるには難しいので $d\tau$ は十分小さく球から見たら $d\tau$ の領域はほぼ中心にあると扱い、 $d\tau$ を光に対して平行な円筒に分割します(蓮コラみたいなのを想像してください)。この時、ある円柱に注目して高さを $ds$ 、断面積を $df$ と表記します。

この時、この円柱 $ds df$ を通過する $dA$ から来る光のエネルギーは次のように表すことができます。ちょっとわかりづらいですが、 $dA$ から見た時の円柱の立体角は $f / r^2$ と表現できることに注意です。

$\displaystyle{ L_\nu d\nu dt \frac{f}{r^2} dA \tag{3.3} }$

こうして円柱に入ってきた光は円柱内である程度の割合で吸収されます。この吸収という過程はボリュームレンダリングにおける吸収と同様であるため、ここで媒質を単位長さ進んだ時の吸収を示す係数として吸収係数 $\mu_a(\nu)$ を導入します。輝度 $L_\nu$ の光が微小長さ $dl$ を進んだ時、吸収される輝度は

$\displaystyle{ L_\nu \mu_a(\nu) dl \tag{3.4} }$

と表すことができます。したがって、円柱 $ds df$ を通過した時、吸収されるエネルギーは $ds$ 分だけ進行したので以下のように表されます。

$\displaystyle{ L_\nu d\nu dt \frac{f}{r^2} dA \cdot \mu_a(\nu) ds \tag{3.5} }$

ここで、領域 $d\tau$ から見た時の $dA$ の立体角 $d\omega$ が $dA / r^2$ であることを使うと

$\displaystyle{ L_\nu \mu_a(\nu) dt d\nu d\omega \cdot df ds \tag{3.6} }$

となります。これを波長で積分すれば、円柱が吸収する光のエネルギーが求められます。

$\displaystyle{ dt d\omega \int_0^\infty L_\nu \mu_a(\nu) d\nu \cdot df ds \tag{3.7} }$

そして $d\tau$ 全体が吸収する光エネルギーというのは各円柱の吸収エネルギーの総和として表されるので各円柱で総和を取ると(円柱同士は被ることはないように分割している)、

$\displaystyle{ d E_{in}(\omega) = dt d\omega \int_0^\infty L_\nu \mu_a(\nu) d\nu \cdot \sum df ds = dt d\omega \int_0^\infty L_\nu \mu_a(\nu) d\nu d\tau \tag{3.8} }$

と得られます。これは要約すると $d\omega$ 方向から来る光を $d\tau$ が吸収したエネルギー $d E_{in}(\omega)$ ということになります。なかなかごちゃごちゃしてきましたが、これをあらゆる方向、つまりは単位球面で立体角積分すると $d\tau$ が吸収する光のエネルギーを求めることができます。

$\displaystyle{ d E_{in} = \int_\Omega d E_{in}(\omega) = 4 \pi d\tau dt \int_0^\infty L_\nu \mu_a(\nu) d\nu \tag{3.9} }$

ようやく $dE_{out}$ と $dE_{in}$ という値が求まりました。熱力学第二法則からこの値は等しいことが要請されるので次のような等式が成立します

$\begin{align} dE_{out} &= dE_{in} \\ 4 \pi d\tau dt \int_0^\infty \epsilon_\nu d\nu &= 4 \pi d\tau dt \int_0^\infty L_\nu \mu_a(\nu) d\nu \\ \int_0^\infty \epsilon_\nu d\nu &= \int_0^\infty L_\nu \mu_a(\nu) d\nu \tag{3.10} \end{align}$

この等式は波長の積分でつながっていますが、例え単波長の光しか存在しない状態でも同様に求められるため、積分の中でも等式が成り立ちます。

$\begin{align} \epsilon_\nu &= L_\nu \mu_a(\nu) \\ L_\nu &= \frac{\epsilon_\nu }{\mu_a(\nu)} \\ \tag{3.11} \end{align}$

$\epsilon_\nu, \mu_a(\nu)$ は一様媒質においては物質の種類と温度のみに依存する値であることから、ある一様媒質内の平衡状態における放射輝度 $L_{\nu}$ は温度 $T$ によって完全に決定され、位置などには依存しないということが求められます。放射輝度 $L_{\nu}$ は一様媒質中では一意的に決められるというわけです。

長々と証明を書いてきましたが、位置依存性がないこと自体は一様性からすでに自明といってもいい感じもありますのであまり嬉しさを感じることはないと思います。（ただ物理学的には結構重要な証明でもあると思います)

(2)無限遠に広がった一様媒質内の散乱

光は真空でない限りは媒質中で散乱を引き起こし、様々な方向へと光が飛び散ります。先ほどまでは吸収と輻射を考えていましたが、今度は散乱が存在した場合について考えていきます。散乱を取り扱うため、今回はある点 $O$ の周囲の微小面積 $dA$ に媒質から放たれた光エネルギーがどれだけなのかについて考えていきます。

$dA$ の垂直方向 $\omega$ から来る光というのは少なくとも微小立体角 $d\omega$ の円錐状に含まれる媒質から放たれたものです。このうち、距離 $r$ から $dr + r$ にある一部の微小体積 $d\tau$ が点O方向へと放つ光のエネルギー $E_{\nu}(\omega,r)$ は放つ輝度を $L_\nu'$ として表すと吸収と同様の議論で

$\displaystyle{ E_{\nu}(\omega,r) = L_\nu' dt d\nu \frac{dA}{r^2} d\tau \tag{3.12} }$

となります。ここで微小体積 $d\tau$

$\displaystyle{ d \tau = r^2 dr d\omega \tag{3.13} }$

と定義されているため、最終的に以下のように書くことができます。

$\displaystyle{ E_{\nu}(\omega,r) = L_\nu' dt d\nu dA dr d\omega \tag{3.14} }$

ここから散乱の効果を踏まえて話していきます。ボリュームレンダリングでもあるように、散乱は輸送する光を散らしたり、逆に他のとこからの光を集めることがあります。すなわち、さらに輻射の他に散乱光のエネルギーが追加されてきます。また、点Oに到達するまで吸収と散乱よって光が減衰していきます。ですが、先んじて結論から述べると平衡状態では散乱があろうとなかろうと実は全く変わらないということが求められます。散乱過程は平衡時には一切何も作用せずいるためには、完全に散乱が起きていない状態と全く同じにならなければならないということです(ある種自明ではある気がしますが)。

実際本当にそうなるのか式で見ていきましょう。ここで散乱係数 $\mu_s(\nu)$ を導入し、散乱による輝度の増加を考えます。平衡状態では前項のように等方的に光が来ており、その内 $\mu_s(\nu)$ の分だけ散乱光のエネルギーとして使用するわけですから、吸収と全く同様の議論で微小体積 $d\tau$ が放つ散乱光の総エネルギー $E_{scatter}(\nu)$ は次のようになります。

$\displaystyle{ E_{scatter}(\nu) = 4\pi \mu_s(\nu) L_{\nu} d\nu dt d\tau \tag{3.15} }$

それで気になるのが散乱の仕方ですが、平衡状態ということを考えれば散乱によるエネルギー差が生まれることはNGなので散乱は一様である必要があります。つまりは、散乱光も方向性を持たず、 $\omega'$ 方向に放たれる散乱光のエネルギー $E_{scatter}(\nu,\omega')$ は単位球面の面積で割ってあげた

$\displaystyle{ E_{scatter}(\nu,\omega') =\mu_s(\nu) L_{\nu} d\nu dt d\tau d\omega' \tag{3.16} }$

となります。よって、先ほどのモデルにおける微小体積 $d\tau$ が $dA$ 方向に放つ散乱光の放射エネルギーは

$\displaystyle{ E_{scatter}(\nu) = \mu_s(\nu) L_{\nu} dt d\nu dA dr d\omega \tag{3.17} }$

という形になります。したがって、 $d\tau$ 全体で輻射と散乱を考えた放射エネルギーについては次のように求めることができます。

$\displaystyle{ E_{\nu}(\omega,r) = \epsilon_\nu dt d\nu dA dr d\omega + \mu_s(\nu) L_{\nu} dt d\nu dA dr d\omega = (\epsilon_\nu + \mu_s(\nu)L_{\nu}) dt d\nu dA dr d\omega \tag{3.18} }$

これが $d\tau$ が点Oに放つ光の放射エネルギーであるが、吸収と散乱によって点Oに至るまでエネルギーが減衰していくことになります。なので、実際 $dA$ が受け取る放射エネルギーはより小さくなっています。減衰の仕方ですが、ここまでで散乱と吸収についてPBRにおけるボリュームと同様に定義してきたおかげで、いつも使ってる一様媒質の減衰として考えることができます。つまりは消散係数 $\mu_a + \mu_s$ によって距離 $r$ に対して指数的 $\exp{-(\mu_a + \mu_s)r}$ に減少します。

$\displaystyle{ E_{\nu}(\omega,r) = (\epsilon_\nu + \mu_s(\nu)L_{\nu}) dt d\nu dA dr d\omega \cdot e^{- (\mu_a + \mu_s)r} \tag{3.19} }$

これでようやく距離 $r$ にある微小体積 $d\tau$ が $dA$ に渡すエネルギーを求めることができました。ここで、 $d\omega$ の円錐内に存在する媒質全ての $\omega$ 方向に渡す光のエネルギー $E_{\nu}(\omega)$ については $r$ を $\lbrack 0,\infty \rbrack$ まで積分することで導くことが可能になります。

$\displaystyle{ \begin{align} E_{\nu}(\omega) &= \int_0^{\infty} (\epsilon_\nu + \mu_s(\nu)L_{\nu}) dt d\nu dA d\omega \cdot e^{- (\mu_a + \mu_s)r} dr \\ &= (\epsilon_\nu + \mu_s(\nu)L_{\nu}) dt d\nu dA d\omega \int_0^{\infty} e^{- (\mu_a + \mu_s)r} dr \\ &= (\epsilon_\nu + \mu_s(\nu)L_{\nu}) dt d\nu dA d\omega \lbrack \frac{- e^{- (\mu_a + \mu_s)r} }{(\mu_a + \mu_s)} \rbrack_0^\infty \\ &= \frac{(\epsilon_\nu + \mu_s(\nu)L_{\nu})}{(\mu_a(\nu) + \mu_s(\nu))} dt d\nu dA d\omega \tag{3.20} \end{align} }$

ここで先ほど求めた(3.11)を用いて輝度 $L_\nu$ を展開すると

$\displaystyle{ \begin{align} E_{\nu}(\omega) &= \frac{\epsilon_\nu}{\mu_a(\nu)} \frac{(\mu_a(\nu) + \mu_s(\nu))}{(\mu_a(\nu) + \mu_s(\nu))} dt d\nu dA d\omega \\ &= \frac{\epsilon_\nu}{\mu_a(\nu)} dt d\nu dA d\omega \\ &= L_{\nu} dt d\nu dA d\omega \\ \tag{3.21} \end{align} }$

となります。式(3.21)を見ると、式に散乱係数 $\mu_\nu$ が打ち消されてどこにも見当たりません。つまり、光のエネルギー輸送において散乱係数に依存せず、「如何なる散乱であっても最終的な状態は全く同じ」ことを意味します。ここで散乱係数が0、つまり散乱が存在しない状態も許容されており、実際(3.20)の時点で代入してもその結果は一致することが確認できます。

$\displaystyle{ \begin{align} E_{\nu}(\omega) &= \frac{(\epsilon_\nu + 0 \cdot L_{\nu})}{(\mu_a(\nu) + 0)} dt d\nu dA d\omega \\ &= \frac{\epsilon_\nu}{\mu_a(\nu)} dt d\nu dA d\omega \\ \tag{3.22} \end{align} }$

すなわち、平衡状態では如何なる散乱過程は何の影響もなく、散乱が存在しないものとして扱っても問題がないことが導かれています。エネルギーの輸送としては、散乱吸収で進むごとエネルギーが減少しますが、その分散乱や輻射によって補填されることで媒質内を一直線に進み続けるとみなして問題がないということになります。

(3) 大きさに制限がある媒質と(1),(2)の関係

長々とクソデカい媒質中の話をしてきましたが、私たちが欲しいのはそんな無限大のものじゃなくて大きさが有限の媒質についての性質です。それに、媒質は1つだけではなく何個も状況でどうなるかということも知りたいわけですよね。

先ほどの状況をもう少し一般的にするため、無限大の媒質を半分に割ってそれぞれ種類が違う媒質に置き換えて、各媒質は片方側だけ無限大というsemi-infinityの状態にした場合を考えます。便宜上、右の媒質を1として左の媒質を2と呼ぶこととします。

ここで媒質1の平衡状態はどうなっているか注目してみます。semi-infinityであるわけですからこの図でいう所の右はいくらでも進むことができ、無限遠方まで進めばその地点はどの方向にも無限遠だけ広がった等方性がある媒質1中にあるとみなすことができます。したがって、無限遠の場所は前項で求めた輝度と散乱の性質が成り立つことが考えられます。

ここで、考える地点を媒質1と2の境界面の方へと近づけていくことを考えます。一見、境界面に近づくほど等方性は崩れていき、infinityにおける性質は成り立たなくなっていくような気がします。

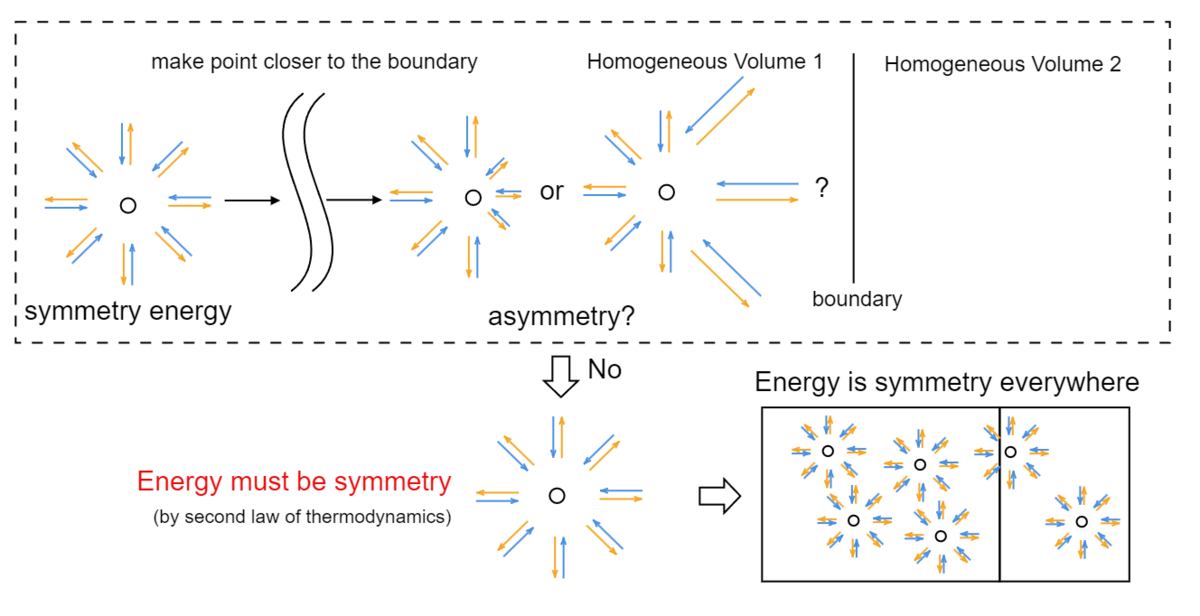
そこで、等方性が崩れ始める位置があると仮定しましょう。そうするとその地点において入ってくる境界面側とinfinity側での輝度はどこかしらの方向で釣り合わない所が出てくるはずです(でなければ等方性は崩れない)。このようなことが起きた場合、境界面側とinfinity側でエネルギーの偏りが生まれることになり、それがドミノ倒しのように様々な所へと影響して平衡状態を解いてしまうことになります。従って、等方性が崩れる境界線というのは存在しないことになります。すなわち、semi-infinityにおいて境界面を含むどのような場所でもエネルギーの等方性が成立し、infinityの場合と同様の平衡状態の性質を持つことが導かれます。

この性質を考えると媒質1をさらにどこかしらで媒質3に置き換えてサンドイッチにした状態で平衡状態にしても同様のことが言え、いくら分割しようとも平衡状態の性質はinfinityと同じことが成り立ちます。つまりは(3.11)と(3.21)の式は有限の大きさの媒質でも成立するということが求められます。

(4) 異なる媒質間における輝度の関係

いよいよキルヒホフの法則の本題に入っていきます。今までの議論により、(3.11)と(3.21)の式は有限の大きさの媒質でも成立し、異なる媒質間の境界面でもエネルギー等方性が成立することがわかりました。とはいえ、境界面は反射や屈折など様々なことが起きているわけですから、それらの結果に等方性が成立するというのはどういう関係性があるのか気になる所です。

ここで、それぞれ屈折率 $\lambda_1,\lambda_2$ が異なる媒質をくっ付けた際の光輸送について考えていきましょう。今回の媒質の境界面は滑らかとして完全な平面であるとします。この際、ガラスに光を通した時と同じでスネルの法則とフレネルの法則に従い境界面では光の反射、屈折が行われているはずです。境界面の微小面積 $dA$ が媒質1側の方向 $\omega$ に輝度[tex: L\nu]の光を放っていた場合、それは媒質1から来た光[tex: L\nu]の反射光と媒質2から来た光tex: L_\nu'の屈折光に由来しています。

ここで反射率 $\rho$ 、媒質2から1の透過率 $1-\rho'$ として、各入射光の方向を $\omega_1,\omega_2$ 、出射方向を $\omega$ とします。先ほどの議論であったように散乱は特に考える必要はなく、これら光にはシンプルにエネルギーとしての釣り合いとして次の等式が要請されます。

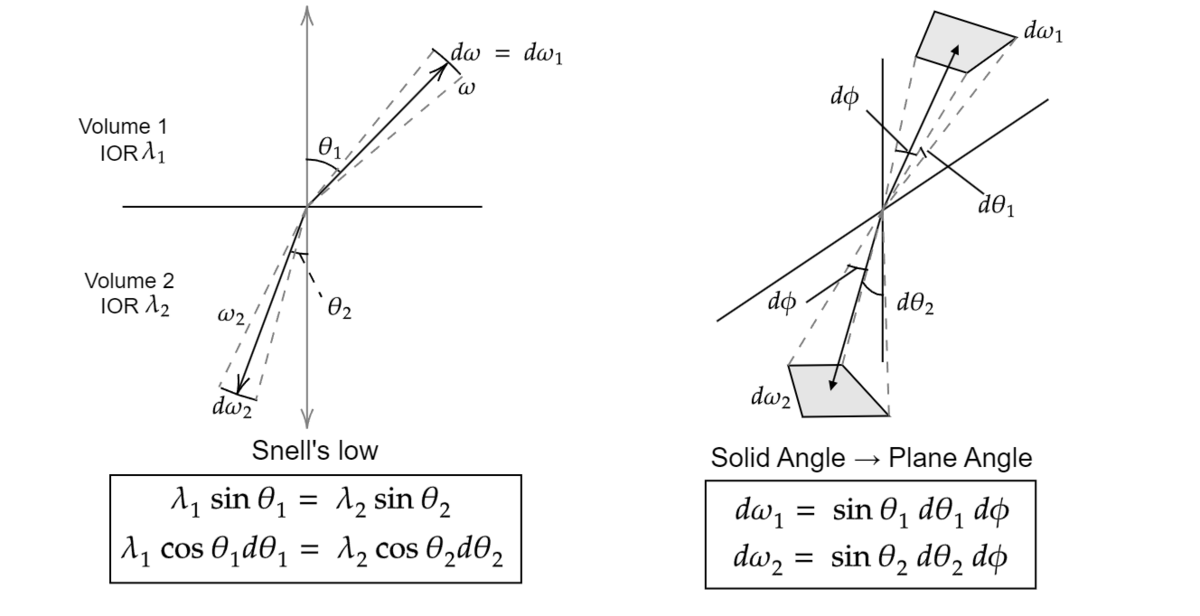
$\displaystyle{ L_\nu \cos{\theta_1} d\omega_1 dt d\nu = \rho L_\nu \cos{\theta_1} d\omega_1 dt d\nu + (1 - \rho') L_\nu' \cos{\theta_2} d\omega_2 dt d\nu \tag{3.23} }$

この式をうまいこと使えるようにするため、立体角 $\omega_1,\omega_2$ の関係について調べていきます。相反性の部分で述べたように光の束は屈折を通すと広がったり集められたりするため、 $d\omega1$ は $\omega_2$ を変化させた関係にあります。ここで一度、立体角を平面角で表現することにします。屈折角、出射角 $\theta$ に対してそれぞれ方位角 $\phi$ を用意してあげると次のように立体角は展開されます。

$\displaystyle{ \begin{align} d\omega_1 = \sin{\theta_1} d\theta_1 d\phi_1 \\ d\omega_2 = \sin{\theta_2} d\theta_2 d\phi_2 \\ \tag{3.24} \end{align} }$

ただし、屈折は同一光平面上で行われる(平たく言えば横に曲がらない)ので方位角方向は変わることがありません。したがって $d\phi = d \phi_1 = d \phi_2$ となります。

ここでスネルの法則

$\displaystyle{ \lambda_1 \sin{\theta_1} = \lambda_2 \sin{\theta_2} \tag{3.25} }$

の両辺を各 $\theta$ で微分すると、 $\theta$ に関する微小量の関係として

$\displaystyle{ \lambda_1 \cos{\theta_1} d\theta_1 = \lambda_2 \cos{\theta_2} d\theta_2 \tag{3.26} }$

と得られます。この等式に立体角の関係を入れれば

$\displaystyle{ \begin{align} \lambda_1 \cos{\theta_1} \frac{d\omega_1}{\sin{\theta_1} d\phi} &= \lambda_2 \cos{\theta_2} \frac{d\omega_2 }{\sin{\theta_2} d\phi} \\ \cos{\theta_2} d\omega_2 &= \frac{\lambda_1}{\lambda_2} \frac{\sin{\theta_2}}{\sin{\theta_1}} \cos{\theta_1} d\omega_1 \tag{3.27} \end{align} }$

ここでスネルの法則から

$\displaystyle{ \frac{\sin{\theta_2}}{\sin{\theta_1}} = \frac{\lambda_1}{\lambda_2} \tag{3.28} }$

が成り立つので最終的に

$\displaystyle{ \cos{\theta_2} d\omega_2 = \frac{\lambda_1^2}{\lambda_2^2} \cos{\theta_1} d\omega_1 \tag{3.29} }$

という立体角の関係性が得られました*8。従って、式(3.23)式は次のように変形することができます。

$\displaystyle{ \begin{align} (1 - \rho) L_\nu \cos{\theta_1} d\omega_1 dt d\nu &= (1 - \rho') L_\nu' \frac{\lambda_1^2}{\lambda_2^2} \cos{\theta_1} d\omega_1 dt d\nu \\ \frac{L_\nu \lambda_2^2}{L_\nu'\lambda_1^2} &= \frac{(1 - \rho')}{(1 - \rho)} \tag{3.30} \\ \end{align} }$

ここで、 $L_\nu,L_\nu'$ は方向依存性がないことが要請されていましたので左辺の値は方向依存性を持ちません。一方で反射率 $\rho,\rho'$ は一般にフレネル係数として方向によって値が変わりますが、左辺に方向依存性がないということから、右辺も同様に $(1 - \rho') / (1 - \rho)$ には方向依存性が存在しないことになります。

$(1 - \rho') / (1 - \rho)$ はどの方向でも値が変わらないということなので、特殊な反射をするブリュースター角度で入射した状況を考えてこの値を求めようと思います。

ブリュースター角は光路面に対して平行な直線偏光(p偏光)が100%透過する特殊な角度のことです。ブリュースター角 $\theta_B$ は1から2に入射する場合は屈折率 $\lambda_1,\lambda_2$ によって、

$\displaystyle{ \tan(\theta_B) = \frac{\lambda_2}{\lambda_1} }$

と定義されています。今までの話で偏光について触れていませんでしたが、一般性を持たせるため暗黙のうちに輝度を円偏光の輝度として扱っていました。本当であれば偏光も踏まえて議論すべきですが、偏光を考えてもこれまで扱っている媒質が等方性を持つため、任意の偏光で今までと同様の議論が成り立ちます。従って、今までの式は偏光状態に依存しないという結論が導かれます(少々話がごちゃつくので省いていました)。なので、さらにp偏光という条件をつけ足して調べてもOKです。

なのでいったんp偏光を当てているとして、 $\omega_1$ の入射角をブリュースター角 $\theta_B$ とした時のことを考えていきます。ブリュースター角 $\theta_B$ で入射した場合、反射率 $\rho$ は完全に0になり $\omega$ 方向に反射光は存在しません。そのため、 $\omega$ 方向の光は対応する $\omega_2$ 方向から来る光によって成り立っています。この $\omega_2$ の入射角については、ブリュースター角の性質として反射方向と屈折方向が直角になるという幾何的性質を持つため、 $\theta_B = 90 - \theta_2$ という関係を持ちます。スネルの法則より、

$\displaystyle{ \frac{\lambda_1}{\lambda_2} = \frac{\sin{\theta_2}}{\sin{\theta_B}} }$

が成り立ち、ブリュースター角との関係式から

$\displaystyle{ \frac{\sin{\theta_2}}{\sin{\theta_B}} = \frac{\sin{\theta_2}}{\cos{(90-\theta_2)}} = \tan{\theta_2} }$

となります。つまり、 $\theta_2$ は媒質2から1への入射時におけるブリュースター角 $\theta_B'$ であることが導かれます。

$\displaystyle{ \tan{\theta_2} = \frac{\lambda_1}{\lambda_2} }$

従って、 $\omega_2$ の入射光の反射率 $\rho'$ も0となることが求められます。よって

$\displaystyle{ \frac{(1 - \rho')}{(1 - \rho)} = \frac{(1 - 0)}{(1 - 0)} = 1 \tag{3.31} }$

が成立します。これは先ほども述べたようにこの値は角度、偏光に依存しません。従って、あらゆる状態において $(1 - \rho') / (1 - \rho) = 1$ が成立することになります。このことから反射率の関係として常に

$\displaystyle{ \rho = \rho' \tag{3.32} }$

という関係式が成り立ちます。ちょっと不思議かもしれませんが、こうなるように(温度依存性を持つので)屈折率が変化していくことで辻褄が合わされていくわけです。

そして、式(3.30)の右辺が常に1であるということなので式(3.30)を変形することで、二つの媒質におけるBasic Radinaceは

$\displaystyle{ \begin{align} \frac{L_\nu \lambda_2^2}{L_\nu'\lambda_1^2} = 1 \\ \frac{L_\nu}{\lambda_1^2} = \frac{L_\nu'}{\lambda_2^2} \tag{3.33} \\ \end{align} }$

と言う等式が成り立ちます。すなわち2つの媒質間でBasic Radianceは常に不変であることが求められたわけです。

これは任意の媒質間で成り立つ等式であることから、熱力学平衡状態においてRadiance Basicは媒質に関わらず任意の場所で同じ値であるということが求められるわけです。従って、キルヒホッフの法則として次の式が得られることになります。

$\displaystyle{ \frac{L}{\lambda^2} = Const. }$

長々と話して来ましたがようやく目標だったキルヒホッフの法則を求めることができました。

相反性の証明

これでBSDFの相反性を証明できる準備が整いました。ここからの証明はとてもシンプルです。

熱力学的平衡状態にある系の任意の隣接する媒質A,Bを取り出して、媒質Aから入射する輝度 $L_1$ の光があるとして、境界面の任意の反射と透過について考えます。

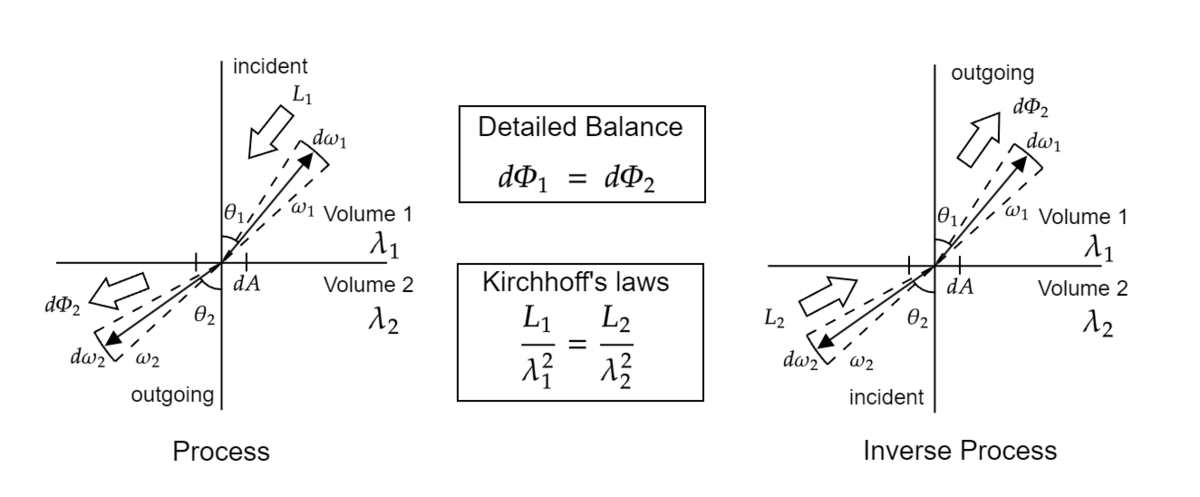
入射光の方向を $\omega_1$ 、ある出射光の方向を $\omega_2$ と表すこととして、出射光の放射束 $d\Phi_2$ については、境界面のBSDF $f(\omega_1,\omega_2)$ を用いて、

$\displaystyle{ d\Phi_2 = d\omega_2 \cos{\theta_2} dA f(\omega_1,\omega_2) L_1 d \omega_1 \cos{theta_1} }$

という風に書くことができます(反射透過問わず)。

この時、 $\omega_1$ から $\omega_2$ へと向かう光に対してDetailed Balanceによって同量の逆過程、 $\omega_2$ から $\omega_1$ へと向かう光が存在します。逆過程における入射光の輝度を $L_2$ として、この過程における出射光 $\omega_1$ の放射束 $\Phi_1$ は

$\displaystyle{ d\Phi_1 = d\omega_1 \cos{\theta_1} dA f(\omega_2,\omega_1) L_2 d \omega_2 \cos{theta_2} }$

と表すことができます。この時Detailed balance により２つの過程は釣り合うことが要請され、その放射束 $\Phi_1$ と $\Phi_2$ はイコールの関係になります。すなわち、

$\displaystyle{ \begin{align} d\Phi_1 &= d\Phi_2 \\ f(\omega_1,\omega_2) L_1 &= f(\omega_2, \omega_1) L_2 \end{align} }$

が得られます。この時、キルヒホッフの法則により、 $\omega_1$ 側と $\omega_2$ 側の屈折率を $\lambda_1,\lambda_2$ と表記すれば

$\displaystyle{ \frac{L_1}{\lambda_1^2} = \frac{L_2}{\lambda_2^2} }$

が成り立ち、先ほどの式に代入するとBSDFの相反性を得ることができます。

$\displaystyle{ \frac{f(\omega_1, \omega_2)}{\lambda_1^2} = \frac{f(\omega_2,\omega_1)}{\lambda_2^2} }$

吸収を考慮した相反性

先ほど述べたキルヒホッフの法則は実は吸収を考慮していないことが指摘されています。先ほどの平衡状態の話にも合ったように物体は基本的に光を当てられた時、吸収という形で光のエネルギーを奪います。その強さを表す量として吸収係数 $\mu_a$ というのを導入していましたが、他にも表現があって消衰係数 $\kappa_a$ というのもあり、光の波長を $\nu$ とすると次のように定義されます。

$\displaystyle{ \kappa = \frac{\nu}{2 \pi \mu_a} }$

それで、これは屈折率 $\lambda$ と合わせて一般的に複素屈折率 $\tilde{\lambda}$ という形で一緒に扱われます。

$\displaystyle{ \tilde{\lambda} = \lambda - \kappa i }$

これ自体は計算を楽にするための便宜上の物理量でそこまで意味はありません(波動の表現で減衰も表示できる)。消衰係数もそれに合わせて作られただけのもので、本質的には吸収係数であることに留意してください。

一般的に物質は特有の消衰係数を持ち、物質中に入った光はその消衰係数に従ってある程度の割合で物質に吸収されていきます。あまり感じることはないですが、空気やガラスなど(誘電体)も物凄く小さい値の消衰係数を持っていたりします。対称的に金属は非常に高い消衰係数を持ち、金属内に入った光は直ぐに吸収されてしまうことが知られています（なので、透明な金属はないですし、内部に入った光が由来のDiffuse光も存在しません）。

この吸収というのがなかなかに厄介な現象を引き起こしがちで、特に今回の話では透過率に大きく影響してきます。吸収を考慮した透過率 $\rho_t$ というのはフレネルによる反射率 $\rho$ に対して次のような性質を持ちます。

$\displaystyle{ \rho_t = (1 - \rho) (1 + \kappa^2) \tag{4.1} }$

$\kappa$ は $\kappa > 0$ として定義されているため、この式は一般的に透過率が $1- \rho$ より増加することを示唆しています。空気やガラスなど誘電体は0.091というような小さな消衰係数を持つのでこの式の影響はほとんどありませんので、厳密に扱わなくても十分とされています。しかしながら、一般的に金属の消衰係数は誘電体に比べはるかに高く、銀とかは波長によりますが5~15という値を持ち(4.1)の値は相当増加することがわかります。

透過率が大きくなるということは、この式によって求められた透過率 $\rho_t$ と反射率 $\rho$ の和は明らかに1を超える $\rho + \rho_t >1$ ことがわかります。どう考えてもエネルギー保存則を破っているように思えるのですが、[Vearch 1997]では透過光の由来の光が入射光と反射光の干渉光であるため、ということである種入射光+反射光の前借り的なことが行われていると説明されており、透過率の増加に伴って他のとこから後々受け取っている(反射率は一時的に大きくなっている)のでエネルギー保存則が満たしている。とのことです。

私はその根拠の元論文は読めなかったのでちょっと懐疑的ですが*9、とりあえずこれを認めて新しいキルヒホッフの法則を求めてみましょう。とはいっても(1)~(3)の話は元から吸収について考えていたので(4)において透過率 $(1-\rho)$ を $(1-\rho)(1+\kappa)$ に置き換えれば問題ありません。なので式(3.30)について、吸収を考えると

$\displaystyle{ \frac{L_\nu \lambda^2_2}{L_\nu' \lambda_1^2} = \frac{(1 - \rho)(1+\kappa^2)}{(1 - \rho')(1+\kappa'^2)} }$

となります。変形すれば、右辺を(3.30)と同様になります。

$\displaystyle{ \frac{L_\nu \lambda^2_2 (1+\kappa'^2)}{L_\nu' \lambda_1^2(1+\kappa^2)} = \frac{(1 - \rho)}{(1 - \rho')} }$

というわけで、同様の議論でブリュースター角の性質を用いれば

$\displaystyle{ \frac{L_\nu}{ \lambda^2_2 (1+\kappa'^2) } = \frac{L_\nu}{ \lambda^1_2 (1+\kappa^2) } }$

が得られるのでキルヒホッフの法則として、媒質の輝度 $L_\nu$ と複素屈折率 $\lambda - i \kappa$ は次のような保存則が成り立ちます。

$\displaystyle{ \frac{L_\nu}{ \lambda^2 (1+\kappa^2) } = Const. }$

これに伴い、Basic Radianceも以上にように定義することができ、BSDFの相反性についても同様に議論すると消衰係数が付いた形で得ることができます。

$\displaystyle{ \frac{f(\omega_1,\omega_2)}{ \lambda^2_1 (1+\kappa^2_1) } = \frac{f(\omega_2,\omega_1)}{ \lambda^2_1 (1+\kappa^2_1) } }$

これに関してはちょっと疑問がありますが、キルヒホッフの法則の修正をすることで新たな相反性を作ることも可能であるわけですね(そういう例としてはいいかもしれません)。

あとがき

ここまで見ていただきありがとうございました&お疲れさまでした

当初は軽い記事の予定だったのですが、書きたいこと書きたいこと増やしていった結果なんかすさまじくデカい記事になってしまいました。一応グラフィックスプログラマーを向けた話のつもりだったのですが、熱力学を平たく言うのが難しくて、結局どこ向けの説明なのか微妙にわからない感じになってしまったのはちょっと反省しています。書いてみると自分の知識不足が露呈していくので大変なことになりますね。

証明はPBR関連の中ではユニークで、結構物理学よりの話となっているのはとても面白いと感じます。学部時代は熱力学いつ使うんだよと思っていましたが、こんな形で使うことになるとは思いませんでした。

正直、誰が見んねんという感じではありますが誰かの役に立てば幸いです

QandA

証明を行っているうえでちょっと気になった疑問と自分なりの解釈を書いておきます(役に立つかはわかりません)

Q 証明では輻射光を対象として考えているが、世間にある光は全部輻射光ではないのでは？
A その通りです。LEDに代表されるように発光ダイオードによる電気的な発光や蛍光塗料のような化学的な発光も存在します。しかしながら、これらがあっても平衡状態では輻射光として見なしてもいいのではないかと思います。

断熱系にこうした光源を置いた時、外部からエネルギーを得られない以上発光するには電池的なエネルギーの蓄えを持つか、系の内部でエネルギーを受け取って循環させる機構が必要になります。前者である場合、平衡状態になるためには蓄えがなくなるまで放出し続けることになり、平衡状態に至る時には既にその発光はもう他の媒質に吸収され輻射光に変換されているでしょう。一方で循環機構があった場合、平衡状態になるには発光する分のエネルギーを何らかの手段で丁度受け取り続けることになります。これは発光の仕組みが違うだけで何ら輻射光がやることと変わりません。

結局のところ、平衡状態では収支が合うエネルギーの輸送をするだけなので、どうやって発光するかについてはどうでもよく、ただエネルギーを受け取りその分だけの光を放つという機構(熱輻射も含め)として釣り合いが生じているということになります。なので輻射光として見なしても問題がない（んだろうな～）と思います。（そもそも区別する必要はない、この説明冗長すぎる）

Q : BSDFは証明が熱平衡状態でやっている以上、ぱっと見た感じ熱平衡状態でしか成り立たないのでは？
A : 熱平衡状態以外でも成り立つ。そもそもBSDFが熱平衡状態かどうかに依存するとしたら、BSDFを構成する微視的領域が系全ての情報を常に同時に知っている(相互作用している)必要があるはずです。もしクソデカ系を考えて、1000光年先の0.0001mm³の部分がちょっと切り取られた時、BSDFが変わるなんてアホみたいなことはないでしょうし。

ちっちゃい領域が自分を含む系が熱平衡かどうかなんか知らないので、BSDFとしては熱平衡、非熱平衡だろうが変わんないわけです。なので熱平衡状態で満たせていれば問題ないです。

Q : BSDFは温度によって変わったりしない?相反性は温度によって変わらない？
A : BSDFは温度に依存する場合は確実にあります。屈折率は少なくとも温度依存性を持つ（陽炎とかはまさにそれ）のでBSDFは温度依存性を持つことになります。今回の議論では温度について特に指定はしていないので、任意の熱平衡状態を扱っており、どんな温度のBSDFでも問題なく相反性が成り立つはずです。
Q : BSDFは本当にどんな状態でも相反性は成り立つの？
A : 微妙な所です。少なくとも今回はDetailed Blanceとキルヒホッフの法則が成り立つことを前提としてしているのでそれが崩れる場合はBSDFも変わる可能性も否定できないです。

Detailed Blanceの根拠となる時間反転対称性ですが電磁気学の基本方程式であるマクスウェル方程式が磁場のある場合、時間反転対称性が崩れるという話もあるのでその場合ってどうなるんじゃろという疑問はあります(ただ、マクスウェル方程式に時間反転対称性を要請するして、もうそれはあるよってことにする立場もあるみたいです)。

ともかく、磁場が顕著に出てくる状況というのは一般的な生活空間ではないですし、3DCGにおけるシーンでは問題なく相反性は成り立つとは思います。

参考文献

[Eric Veach 1997] ROBUST MONTE CARLO METHODS FOR LIGHT TRANSPORT SIMULATION

[Lazányi, I. and Szirmay-Kalos, L. 2005] Fresnel term approximations for metals.

RAY TRACING GEMS Ⅱ

熱輻射論講義マックス・プランク著, 西尾鳴子訳, 岩田書店

熱力学押田勇雄藤城敏幸著

双方向(反射率|透過率|散乱)分布関数 (B(R|T|S)DF) - Computer Graphics - memoRANDOM

Open PBR https://academysoftwarefoundation.github.io/OpenPBR/

ＦＮの高校物理キルヒホッフの法則（熱的放射平衡における　1859～1860年）キルヒホッフの法則（熱的放射平衡における 1859〜1860年）

基礎方程式の時間反転対称性 - YouTube

【量子力学・デジタル】時間反転（古典） - YouTube

学習院大学理学部物理学科田崎晴明氏現代科学「ミクロとマクロの物理学」なぜ時間に向きがあるのだろう？ https://www.gakushuin.ac.jp/~881791/materials/Irreversiblity09.pdf

大学共同利用機関法人 KEK 時間の向きを逆にしても同じこと？時間の向きを逆にしても同じこと？？

29.2: The Principle of Detailed Balance - Chemistry LibreTexts

Wikipedia Detailed Balance Detailed balance - Wikipedia

Wikipedia Etendue Etendue - Wikipedia

*1:エーテル仮設という昔の光の仮説に出てくるものです。波は一般的に媒質を要求しますが(今では違う気がしますが)、電磁波は媒質が存在しない真空中でも存在するということが確認されています。この矛盾に対する仮説として、私たちが認知していないだけで電磁波の媒質、エーテルが宇宙で充填されているのではないかという感じで出てきたものです。現在では否定されている説ですが、当時は有力な説として扱われていました。

*2:キルヒホッフの法則はいくつもあります。多分一般的にはキルヒホッフの法則といえば電流の法則を指すと思いますが、ここでは熱輻射に関するやつを単にキルヒホッフの法則と呼びます。

*3: カロリックという考え方自体は古代からあったみたいです(四大元素もそれに近い概念?)

*4:これがエントロピー増大則です。状態の変化は可逆か非可逆かの二通りあり、可逆だとエントロピーは変化せず、非可逆過程だとエントロピーが増大するためエントロピーは基本的に増加していくというのを数式的に表現されています

*5:電磁気学は磁場が存在する場合、実は時間反転対称性を持たないことが知られています。ですが、マクスウェル方程式は時間反転対称性を持つと要請して磁場の方を修正するというような方式もあり、色々とややこしい話がいっぱいあります。少なくとも磁場がなければ、問題なく可逆であるといえますのであまりここでは触れないでおきます(よくわからないし...)

*6:ただし、媒質は等方的であるという条件があります

*7: 調べた感じ一般的に熱輻射のキルヒホッフの法則はこの形ではなく更に吸収能、放射能という量に対する関係式として表されています。一応[Veach 1997]に従い、この形式をキルヒホッフの法則と呼ぶこととします(等価な式のはずだし)。

*8: この関係性を利用して補正をかけた面積、立体角をEtendueという量として定義されることもあります。Basic Radianceの保存もEtendueの保存則として定義するというお作法もあるみたいです。

*9:複素屈折率を考慮したフレネルは反射率だけは求められていますがあんまり透過率について議論されていない気がします。少なくともPBRの分野ではとやかく言われていないので、ガチガチの光学に行かないと真相はわからなさそうですね...

MochiMochi3D

3D関係の記事を書きます

BSDFの相反性(Reciprocity)