初めに

この記事はレイトレ合宿8 アドベントカレンダー7/17の２個目の記事です。

パストレーシングにおいて効率的にCausticsをレンダリングすることができるManifold Next Event Estimation(MNEE)という手法とそれの発展手法である Specular Manifold Sampling(SMS)を先行手法のManifold Exploration(Manifold Walk)と共に大まかに解説する記事となっています。

初めに
CausticsとPathTracing
PathTracingでCausticsを出す手法
Manifold Exploration
Manifold Next Event Estimation
- MNEEの問題点
Specular Manifold Sampling
- unbias SMS
- Bias SMS
実装の資料
おわりに
参考文献、引用論文

CausticsとPathTracing

Caustics(集光模様)とは複雑な曲面による反射、屈折によってできる光の模様のことです。Causticsは日常生活でも簡単に見られ、水の入ったグラスやペットボトルに光を当ててみると非常に複雑で美しい光の模様(Caustics)を見ることができます。ほかにもきれいな海の底にはよくCauticsが現れていて、絵的に映えるエフェクトの一つです。

実際に水が入ったグラスやペットボトルに光を当ててみるとCauticsが出てきます。

Causticsが生まれる流れを見てみましょう。ガラスを通した光というのは屈折によりその経路を曲げられてしまいます。ガラス面が複雑だと例え平行光を当てたとしても、屈折によってさまざまな方向へと光が曲げられてしまうわけです。そうすると地面には光が集まりやすい場所と逆に光が全然集まらない場所というように光の偏りが生まれ、結果としてCauticsとして我々は光の模様を見ることになります。すごい簡単なイメージとしては虫眼鏡で光を集めるようなものです。

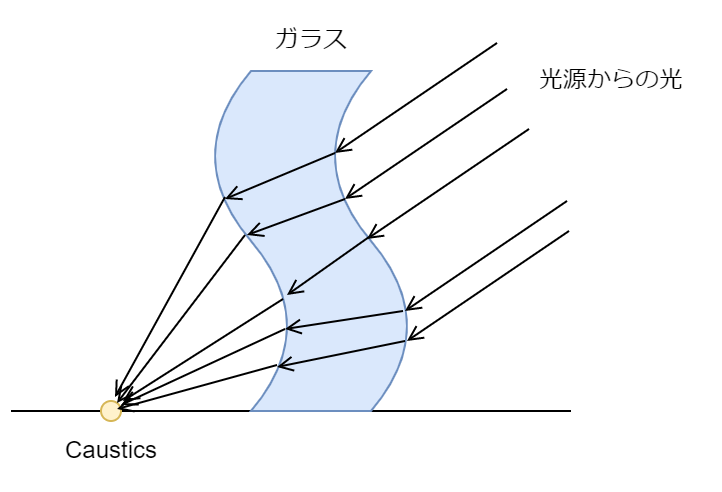
Cauticsは水やガラスなど屈折する物体が支配的なシーンだと絵的な部分で非常に重要なエフェクトになります。なので是非ともレイトレでこのCauticsを出したいところなのですが、実は問題があります。凹凸が激しい理想反射面が存在するシーンを用意し、純PathTracingを1000spp程度で行うと以下のようにファイアフライが強く現れます

PathtracingのCausticsレンダリング [Zeltner et al. 2020] movieより引用

これはBRDFからサンプリングする方向がCausticsの経路と全くの無関係であるためです。レイがスペキュラー面を通った上で”偶然”光源に当たることでしか寄与を得ることができません。しかも、間にスペキュラー面が入ることで寄与が高い経路が指向性を持つことになるため、このようなひどいノイズが生まれるわけです。明示的に光源とサンプリング点をつなげる手法としてNEEがありますが、通常のNEEだとまっすぐにパスをつなげることになるのでこのような屈折反射を考慮したパスというのは生成できません。このように単純なPathTracingでは実用的にはCauticsを出ことができません。

Cauticsは視点からの探索では難しいのですが、一方で光源側から探索する場合には簡単です。そのため、光源側からもパスを作るBDPT(BiDirectional Path Tracing)や光源からフォトンを飛ばすフォトンマッピングはこのCauticsを綺麗に出すことが可能な手法として知られています。

#raytracing #cpp #3dcg #pbr #rendering
自作レンダラーにVolumetric progressive photon mappingを実装して水入りコーネルボックスをレンダリングしてみた。Causticsと水の質感がめちゃくちゃ綺麗に出てくれて楽しい pic.twitter.com/3BumMWhUkS
— yumcyawiz🍵 (@yumcyawiz) 2021年12月19日

これらの手法は静止画においては非常に強力な手法ですが、アニメーションの分野に入ってくると話が変わります。この手法をアニメーションのレンダリングを行うとメモリや目立つノイズなどのアニメーション特有の問題点が現れ、これら手法をそのままアニメーションレンダリングに使うことは難しいとされ[Hanika et al. 2015]、多くのアニメーションを前提とする商用レンダラーではあまり採用されていません（多分）。対照的に PathTracingはアニメーションレンダリングにおいて安定したレンダリングを行うことができ、多くの商用レンダラーではPathTracingを採用しています。こうした理由から動的なCausticsレンダリングを行うには、新しくPathTracingの枠組みの中で効率的にCausticsを出す手法を見つけ出す必要があります。

PathTracingでCausticsを出す手法

　話はちょっと変わって最近Blenderがバージョンアップして3.2になり、目玉機能としてShadowCausticsと呼ばれる機能が追加されたとのことでした。これは何だろうとみてみたところなんとCausticsを出すことができるものでした。色々とShadowCausticsに関する動画はいっぱいありましたが、見た感じちゃんとしたCausticsを出すことができるっぽいです。

www.blender.org

実際にやってみると以下のようになりました。同じシーンで大体同じ秒数でShadowCausticsなしとありで比べています。

こうしてみるとちゃんと実用的な形でCausticsを出していることがわかります。BlenderのCyclesはPathTracerのはずなので遂にPathTracerでCausticsが出せるようになったんだと感じました。

　こんなことがあり、どうやってこんなん実装してるんだろうということで調べたところ[Hanika et al. 2015]"Manifold Next Event Estimation"(MNEE)という手法を使っているということがわかり、レイトレ合宿もあるので折角なので実装目当てで周辺論文含め色々調査してみました。今現在もまだいまいち実装まで漕ぎつけていませんが、大まかな内容をまとめるため記事にしたという次第です。

　結構元論文[Hanika et al. 2015]は先行論文を読んでいることが前提のような書き方であり、実装も（なぜかBlenderも含め）見当たらず中々探るのは難しかったのですが、MNEEの改良を行った[Zeltner et al. 2020]"Specular Manifold Sampling"(SMS)という論文ではMNEEを含め先行研究をまとめており、なおかつ実装などの資料が豊富であったためこちらの論文を主に探りつつほかの論文を調べていきました。

　そういう感じでMNEE及びSMSの周辺論文をまとめると

[Jakob Marschner et al. 2012] Manifold exploration
[Jakob 2013] Light Transport On Path-Space Manifolds
[Kaplanyan et al. 2014] The natural-constraint representation of the paath space for efficient light transport simulation
[Hanika et al. 2015b] Improved Half Vector Space Light Transport
[Hanika et al. 2015a] Manifold Next Event Estimation
[Zeltner et al. 2020] Specular Manifold Sampling

というような流れで作られていると思われます。特にManifold explorationについてはMNEE及びSMSの根幹的な手法であるため、この記事ではManifold explorationを含めMNEEとSMSについて簡単にまとめて行こうと思います。

Manifold Exploration

Manifold Explorationは[Jakob Marschner et al. 2012]にて発表された手法です。この論文では純モンテカルロ法ではなく、MCMC（マルコフ連鎖モンテカルロ法）で扱う形になっていますが、ここで提唱されたManifold Exploration自体は後々の論文で基礎的手法として使われています。ちなみにJakobさんの博論[Jakob 2013]はこれをより詳細に述べているので調べる際はこちらの方が良いかと思います。

この手法はSpecular Manifoldと呼ばれるものを定義し、ガラスなどを通るような現在のパスを少し動かし、物理的に成立する新たなパスを発見する方法です。

Specular Manifold

図のようなLDSDEパスを作ったものとして、スペキュラー面は理想的な反射、屈折を行うもののみ(glossyはなし）を考えます。この際、スペキュラー面Sでは $x_2$ から来た光は $x_3$ に当たり、反射することで $x_4$ に向かいます。この反射は当然皆さんが知る通り、スペキュラー面の法線 $N(x_3)$ との入射角、反射角が等しくなるように設定されています。

当然と言えば当然なのですが、これは（理想反射の）スペキュラー面を通るパスに必ず課せられる条件となります。これを逸脱することは物理的にあり得ない光の軌道となってしまいます（フェルマーの原理に違反する）。

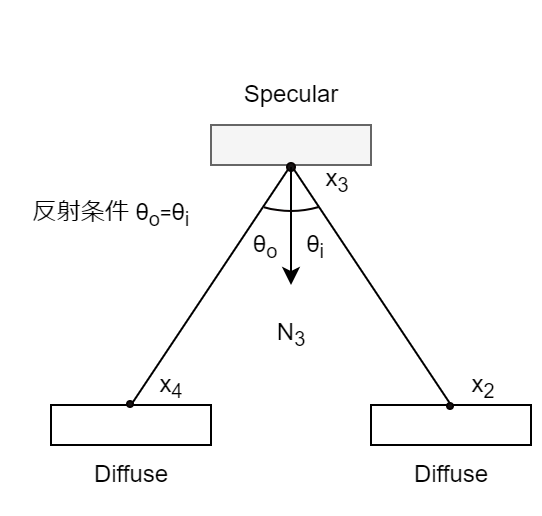
この制約から反射先である $x_4$ というのは $x_2,x_3$ から決定されることから、このパスというのは $x_4$ の部分を取ったより低い次元で考えることができます。従って、スペキュラーが入っているパス空間 $\mathcal{P}$ はスペキュラーの制限が入ったより低い空間、Specular Manifold $\mathcal{S}$ で考えることができるというわけです。

なので、（あくまでスペキュラー面を通る）上記の例のパス空間 $\mathcal{P}$ は以下のようなSpecular Manifold $\mathcal{S}$ に落とし込むことができます。次元は $\mathbb{R}^{10}$ から $\mathbb{R}^{8}$ へとなっているはずです。（各点は何かしらの表面つまり多様体上にあるため、座標の自由度は２になる）

$\displaystyle{ \mathcal{S} =\lbrace ([ (x_1, x_2, x_3, x_4 ,x_5) \in \mathcal{P} | (\vec{x_2 x_3} + \vec{x_3 x_4}) // N(x_3) \rbrace }$

[Jakob Marschner et al. 2012]ではこのSpecular Manifoldを一般的に定義し、そこから近傍のパスの探索へと発展させています。

一般の場合を考え、長さnのパス $\bar{\bf{x}}$ があるとして、各頂点を $x_1,x_2,...,x_i,...,x_n$ としておきます。各スペキュラーS上の点 $x_i$ には先ほどの反射、屈折の法則から前の点 $x_{i-1}$ と次の点 $x_{i+1}$ の間には位置座標に制約がかけられます。この制約をある関数 $c$ として表すこととして、 $x_i,x_{i-1},x_{i+1}$ の制約を

$\displaystyle{\begin{align} c_i(x_{i-1},x_i,x_{i+1}) \left\{ \begin{array}{} = 0 &(反射屈折の条件を満たしている）\\ \neq 0 &(otherwise) \end{array} \right. \end{align} } \tag{1.1}$

と関数を使って表現します。この制約関数は $x_i,x_{i-1},x_{i+1}$ が反射、屈折の条件を満たしていれば０，満たしていない時０以外を返します。こうしておくことで、スペキュラーを通るパスというのが制約関数 $c$ の解として表現できるというわけです。

それはよいのですが、実際このような制約関数 $c$ はどうやって作るのかというとハーフベクトルと法線の関係を用います。[Jakob Marschner et al. 2012]では以下のように制約関数 $c$ を定義しています。

$\displaystyle{\begin{align} \ c_i(x_{i-1},x_i,x_{i+1}) = T^T(x_i) h(x_i,\vec{x_i x_{i-1}},\vec{x_i x_{i-1}}) \tag{1.2}\\ \\ \ h(x,\omega,\omega') =\frac{n(x,\omega) \omega + n(x,\omega') \omega'}{||n(x,\omega) \omega + n(x,\omega') \omega'||} \end{align} }$

$h$ は単に $x_i,x_{i-1},x_{i+1}$ のハーフベクトルを返す関数で二番目の式のように作られています。nはそれぞれ境界面の屈折率で屈折におけるハーフベクトルも同様に扱えるようになっています。

要としては $T(x_i)$ ですが、これは点 $x_i$ の接空間のtangentとbinormalの基底ベクトルで作られた接平面への投影行列です。具体的な表現としては $x_i$ のtangent基底を $(t_{xi}, t_{yi}, t_{zi})$ ,binormalの基底を $(b_{xi}, b_{yi}, b_{zi})$ 、ハーフベクトルを $(h_{xi},h_{yi},h_{zi})$ とすれば

$\displaystyle{ c_i(x_{i-1},x_i,x_{i+1}) = \begin{pmatrix} t_{xi}& t_{yi}& t_{zi}\\ b_{xi}&b_{yi}& b_{zi} \end{pmatrix} \begin{pmatrix} h_{xi} \\ h_{yi} \\ h_{zi}\\ \end{pmatrix} }$

となっています。なので制約関数 $c$ は二次元ベクトルとなっています。図的なイメージとしては以下のようにtangent,binormalで作るtangent planeにハーフベクトルを $h_i$ が落とした影のベクトルが $c$ というわけです。

接空間は法線 $n$ が一つの直行基底ベクトルなわけですから、tangent plane上に投影すると０ベクトルになることがわかります。従って $h$ が以上の投影で０ベクトルになるということは法線と平行であることを示し、ちゃんと制約関数は(1.1)を満たしていることになります。

ここで長さ $n$ のパス $\bar{\bf{x}}$ の内、p個の頂点はスペキュラー面Sに存在するとします。この時、スペキュラー面にある各点はおのおの制約関数 $c$ の条件を満たしている必要があり、これをパス全体の制約としてパスの制約関数 $C$ を考えることができます。ということで一般的なSpecular Manifoldは以下のように定義することができます。

$\displaystyle{ \mathcal{S} =\lbrace \bar{\bf{x}} | C(\bar{\bf{x}}) = 0 \rbrace } \tag{1.3}$

　長々とSpecular Manifoldの定義をやってきましたが、このような定義にしたのはSpecular Manifoldのパラメトライズを行うためです。

　パス制約関数 $C(\bar{\bf{x}})$ は実質的に各頂点の陰関数として表現されており、その陰関数が作る多様体がSpecular Manifoldとなっています。また、ジオメトリ上の点の集まりでしかないためパス制約関数 $C(\bar{\bf{x}})$ は微分が可能です。　このことからパス制約関数 $C(\bar{\bf{x}})$ に対して陰関数定理を適用でき、ある特定のパス近傍でパラメトライズが保証されることになります。これは何が言いたいかというとある頂点 $x_i$ を使ってほかの頂点を $x_i$ の関数として $x_k(x_i)$ として表現できることが保証されていることを示しています（多分）。

　今あるパスの頂点 $x_i$ をちょっと動かした新しいパスが欲しいなというときにパス制約関数 $C(tex: \bar{\bf{x}}$ をちゃんと満たすパスの他の頂点を数値的に計算することが可能である、つまり近傍のパスの探索を行うことができるわけです。

　SpecularManifold上ではDiffuseの点が決定すると、Specular上の点はそれらの点から自動的に決まります。このため、このパラメトライズは $(n-p)$ 個のDiffuse点 $\mathbb{R}^{2(n-p)}$ からSpecular点 $\mathbb{R}^{2p}$ を求める関数 $P$ とみなすことができるわけです（ただし現在のパス近傍限定）。

　 $P$ の微分は多様体の接空間を与えており、これは $C$ の微分から得ることができます。そのため、 $C$ の微分 $\nabla C$ を計算していく必要があります。

具体的な例

もう少し具体的な状況として図のようなパスを考えます。

このパスは $x_1,x_2,...,x_7$ と各頂点がつなげられており、その内 $x_2$ から $x_6$ はスペキュラー上に存在します。このようなパスに対してパス制約関数 $C$ はそれぞれの各点の制約関数 $c_i$ を集めた行列として考えることができます。

$\displaystyle{ C(\bar{\bf{x}}) = \begin{pmatrix} c_2(x_1,x_2,x_3) \\ c_3(x_2,x_3,x_4) \\ ...\\ c_6(x_5,x_6,x_7) \end{pmatrix} }\tag{1.4}$

この $C$ に対して微分 $\nabla C$ を考えます。 $\nabla$ の中身は各頂点の微分が入っており、その微分は以下のような5×7行列として書き下すことができます。

$\displaystyle{ \nabla C(\bar{\bf{x}}) = \begin{pmatrix} \frac{\partial c_2}{\partial x_1} & \frac{\partial c_2}{\partial x_2} & \frac{\partial c_2}{\partial x_3} & \frac{\partial c_2}{\partial x_4} & \frac{\partial c_2}{\partial x_5}& \frac{\partial c_2}{\partial x_6} &\frac{\partial c_2}{\partial x_7}\\ \frac{\partial c_3}{\partial x_1} & \frac{\partial c_3}{\partial x_2} & \frac{\partial c_3}{\partial x_3} & \frac{\partial c_3}{\partial x_4} & \frac{\partial c_3}{\partial x_5}& \frac{\partial c_3}{\partial x_6} &\frac{\partial c_3}{\partial x_7}\\ \frac{\partial c_4}{\partial x_1} & \frac{\partial c_4}{\partial x_2} & \frac{\partial c_4}{\partial x_3} & \frac{\partial c_4}{\partial x_4} & \frac{\partial c_4}{\partial x_5}& \frac{\partial c_4}{\partial x_6} &\frac{\partial c_4}{\partial x_7}\\ \frac{\partial c_5}{\partial x_1} & \frac{\partial c_5}{\partial x_2} & \frac{\partial c_5}{\partial x_3} & \frac{\partial c_5}{\partial x_4} & \frac{\partial c_5}{\partial x_5}& \frac{\partial c_5}{\partial x_6} &\frac{\partial c_5}{\partial x_7}\\ \frac{\partial c_6}{\partial x_1} & \frac{\partial c_6}{\partial x_2} & \frac{\partial c_6}{\partial x_3} & \frac{\partial c_6}{\partial x_4} & \frac{\partial c_6}{\partial x_5}& \frac{\partial c_6}{\partial x_6} &\frac{\partial c_6}{\partial x_7}\\ \end{pmatrix} }\tag{1.5}$

各 $c$ で依存しない頂点の微分を０にすれば、

$\displaystyle{ \nabla C(\bar{\bf{x}}) = \begin{pmatrix} \frac{\partial c_2}{\partial x_1} & \frac{\partial c_2}{\partial x_2} & \frac{\partial c_2}{\partial x_3} & 0 & 0 & 0 & 0 \\ 0 & \frac{\partial c_3}{\partial x_2} & \frac{\partial c_3}{\partial x_3} & \frac{\partial c_3}{\partial x_4} & 0 & 0 & 0 \\ 0 & 0 & \frac{\partial c_4}{\partial x_3} & \frac{\partial c_4}{\partial x_4} & \frac{\partial c_4}{\partial x_5}& 0 & 0\\ 0 & 0 & 0 & \frac{\partial c_5}{\partial x_4} & \frac{\partial c_5}{\partial x_5}& \frac{\partial c_5}{\partial x_6} &0 \\ 0 & 0 & 0 & 0 & \frac{\partial c_6}{\partial x_5}& \frac{\partial c_6}{\partial x_6} &\frac{\partial c_6}{\partial x_7}\\ \end{pmatrix} }\tag{1.6}$

というように書くことができます。この微分はSpecular Manifoldにおいて様々な情報を持ち、2 ~ 6列というのは特にスペキュラー面に関する情報を持ちます。ということでDiffuse点の微分である1,7列目部分を $B_1,B_7$ 、Specular点の微分である $A$ で行列を分けることとします。

$\displaystyle{ B_1 = \begin{pmatrix} \frac{\partial c_2}{\partial x_1} \\ 0\\ 0\\ 0\\ 0 \end{pmatrix} ,A = \begin{pmatrix} \frac{\partial c_2}{\partial x_2} & \frac{\partial c_2}{\partial x_3} & 0 & 0 & 0 \\ \frac{\partial c_3}{\partial x_2} & \frac{\partial c_3}{\partial x_3} & \frac{\partial c_3}{\partial x_4} & 0 & 0 \\ 0 & \frac{\partial c_4}{\partial x_3} & \frac{\partial c_4}{\partial x_4} & \frac{\partial c_4}{\partial x_5}& 0 \\ 0 & 0 & \frac{\partial c_5}{\partial x_4} & \frac{\partial c_5}{\partial x_5}& \frac{\partial c_5}{\partial x_6} \\ 0 & 0 & 0 & \frac{\partial c_6}{\partial x_5}& \frac{\partial c_6}{\partial x_6} \\ \end{pmatrix} B_7 = \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ \frac{\partial c_6}{\partial x_7} \end{pmatrix} }\tag{1.7}$

これらを用いると、SpecularManifoldのtangent spaceを以下のように求めることができます。（ここの理由はちょっとわかんないです）。

$\displaystyle{ T_{\mathcal{S}}(\bar{\bf{x}}) = - A^{-1} (B_1,B_7) } \tag{1.8}$

これは、 $(7 - 2) \times 2$ の行列で各列はDiffuse点 $x_1,x_7$ に関する各点の微分の値を示しています（ $P$ の $x_1,x_7$ 微分とも取れる？）

$\displaystyle{ \frac{ \partial \begin{pmatrix} x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \end{pmatrix} }{\partial x_1} = - A^{-1} B_1 , \frac{ \partial \begin{pmatrix} x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \end{pmatrix} }{\partial x_7} = - A^{-1} B_7 } \tag{1.8}$

この結果は、 $x_1$ が少し動いたとき、 $x_2,...,x_6$ はどれだけ動くのかということを(1.8)によって求めることができることを示しています。すなわちちゃんとSpecular Manifoldのパラメトライズができていることになります。ちなみに $A$ について逆行列を求めていますが、 $A$ は式(1.7)のように三重対角行列行列のため、実装にそこまで計算の負担にはなりません。

Manifold Exploration

　以上によってSpecular Manifoldのパラメトライズなどをお話していきましたが、結局のところ何がしたいのかというと、こうしたパラメトライズをすることでパスの探索に役立てることができるというわけです。

　例えばですが、終点のDiffuse点 $x_7$ ではなく、特定の点 $x_7'$ にパスの終点を移動させたい場合を考えます。この場合、通常のパストレだと $x_7'$ に狙って当たるように $x_1$ のサンプリングを変えることはできないので、この問題は難しいものとなります。

　しかし、今まで考えてきたManifold Specularと $\nabla C$ の値から我々は $x_7$ に関するパラメトライズができるようになっています。 $x_7$ を $x_7'$ に移動させた時、Specular上の点 $x_2, ... ,x_6$ はどのように移動すればいいかは(1.8)より、

$\displaystyle{ \frac{ \partial \begin{pmatrix} x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \end{pmatrix} }{\partial x_7} T(x_7)^T (x_7' - x_7) =x_7がx_7'に移動するのに必要な他の点の移動量 } \tag{1.9}$

として求めることができるわけです（ $T(x_7)^ T$ を挟んでいるのは、あくまでこのパラメトライズが"tangent空間でのパラメトライズ"のためで））。これにて新しくできた $x_2^+$ 方向に $x_1$ からサンプリングすると $x_7'$ に到着するパスが出来上がるわけです。

　このようにSpecular Manifoldを使うことで新たなパスを効率的に求めることができ、この手法をManifold Explorationと呼びます。論文内ではアルゴリズムそのものはManifold Walkと呼んでたりします。

　それでは実際にManifold Walkの疑似コードを見ながら、どのような処理でこれができるのかを見ていきます。

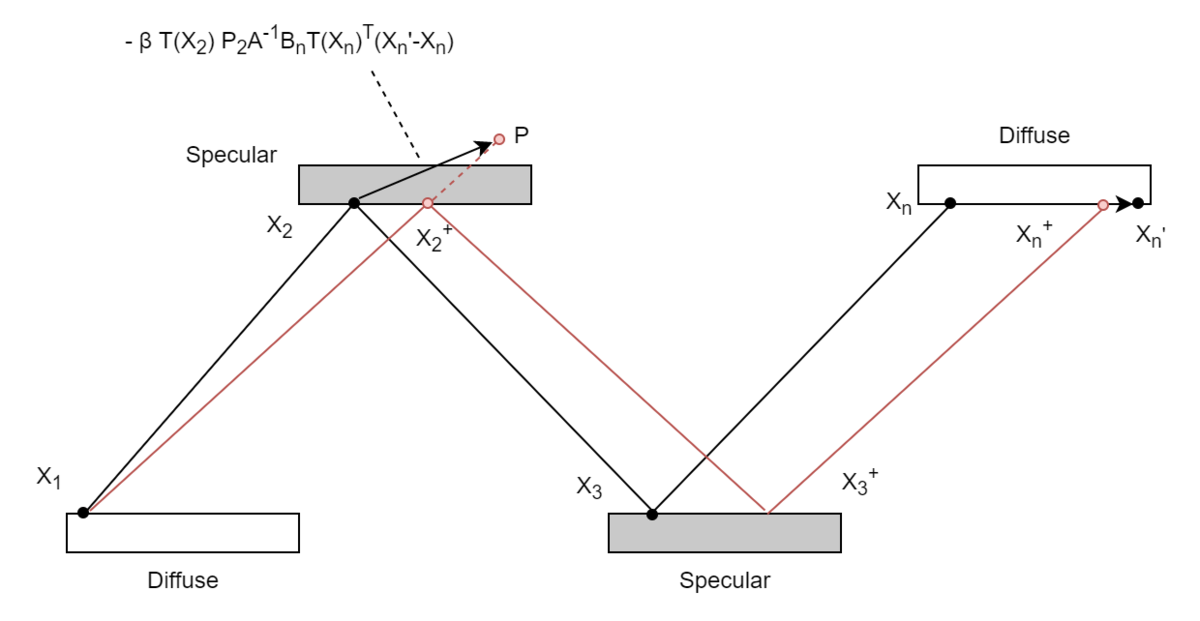
　 $x_1 ~ x_n$ の頂点があるとして、終点である $x_1,x_n$ はDiffuse点で他の点はすべてスペキュラー上の点として考えています。このManifold Walkは終点 $x_n$ を $x_n'$ という新しい点へと移動させるということを考えています。

　 $i$ はイテレーションであり、 $\beta$ はManifold Walkにおけるステップの度合を管理するものでこれが大きければステップにおける移動量が大きくなります（初期値は１）。

Line2~3

　2よりManifold Walkの処理が開始します。このWhile文は更新していった $x_n$ の位置がターゲット $x_n'$ に非常に近くなった時に成功とみなし、 $N$ 回行ってもこれを満たさなかった場合は失敗という形でループを構成しています。

　まず、Line3にて複雑な式で新しい点 $p$ を生成していますが、一つ一つほどくと $p$ の意味が分かります。まず、マイナス部分と合わせて $- A^ {-1} B_n T(x_n)^ T (x_n' - x_n)$ の部分というのはこれは式(1.8)と(1.9)から" $x_nからx_n'へと移動させたい時に必要な他の頂点のタンジェント空間上での移動量$ "を意味しています。つまり $p$ は何らかの頂点を移動させた結果なわけであります。

　今回、Ideal Specularのみを考慮しているため、Specular上の点は１つでも決まればそこから明示的に他が決定するため、 $x_2$ についてのみの移動さえ考えればいいわけです。ということで先ほどの移動量から $x_2$ に関するもののみを取り出す $P_2$ という行列をかけて、 $x_2$ の移動量を求めているわけです。この移動量はタンジェント空間におけるものなのでワールド空間上への移動量にするため $T(x_2)$ を挟んで最終的に必要な $x_2$ を得ているわけです。最後に移動量にβをかけていますが、単に移動量を調節するために入れているだけです。

　以上のことから、 $p$ が意味することは"点 $x_n$ が $x_n'$ へと移動すると考えられる新しい $x_2$ の位置"であることがわかると思います。

Line4

　ただし、 $p$ の計算はあくまでManifold Specular上で行われているため、実際のGeometry上の点ではありません。なので正しい値にするため、 $x_1$ から $p$ 方向にレイを飛ばし、新たなパス $x_1, x_2^+,x_3^+,...,x_n^+$ をLine4で生成しています。

　この新しいパスの終端 $x_n^+$ はおおよその場合で完璧ではないものの $x_n'$ に近づきます（Manifoldの計算のため)が、必ずしもというわけではなく、移動量が多すぎて $x_n'$ を通り過ぎてしまう場合があります。この場合分けをLine5,Line8で行っています。

Line5 ~ 9

　 $x_n^+$ が $x_n'$ にちゃんと近づいている場合は現在のパス $x_1,x_2,...,x_n$ の値を $x_1,x_2^+,...,x_n^+$ へと更新して、同様の探索を再び行っていきます。

　一方で $x_n^+$ が $x_n'$ から離れてしまうということはこれは移動量が多すぎて、 $x_n^+$ が $x_n'$ を飛び越してしまう状況です。なので移動量の度合 $\beta$ の値を小さくし、再び同じように探索を行わせることで、別のパスを調べていくことになります。

　以上が大まかなアルゴリズムの説明で、こうすることでSpecular Manifold上で新しいパスをある程度指定して探索することができます。[Jakob 2013]ではあくまでこの探索法をMCMCで使用していましたが、後年ではPathTraceにこの方法が応用されMNEE,SMSへと使われていくこととなります（多分）。また、この手法は $C$ の解を数値的に求めているニュートン法に近く、後の論文ではこの手法をニュートン法として述べているものもありました。

Cの微分の計算

　Manifold walkを行うのに一番重要なのは $C$ の微分 $\nabla C$ の計算で、これをどうやって計算するかという問題がまだ残っています。例として、最も簡単なSpecular chainを考えます。 $x_1,x_2,x_3$ の頂点があり、 $x_1,x_3$ はDiffuse点、 $x_2$ はSpecular点とみなします。この際の $C$ は $x_2$ 点に関する $c_2(x_1,x_2,x_3)$ となります。

　この時の $C$ の微分 $\nabla C$ は、以下のように示されます。

$\displaystyle{ 　 \nabla C = (\frac{\partial c_2(x_1,x_2,x_3)}{\partial x_1},\frac{\partial c_2(x_1,x_2,x_3)}{\partial x_2},\frac{\partial c_2(x_1,x_2,x_3)}{\partial x_3}) } \tag{1.10}$

$c_2$ について、式(1.2)より書き下すと各微分について依存する変数で以下のようになります。

$\displaystyle{ 　 \nabla C = (T(x_2)^T \frac{\partial h(x_1,x_2,x_3)}{\partial x_1},T(x_2)^T \frac{\partial h(x_1,x_2,x_3)}{\partial x_2} + \frac{\partial T(x_2)^T}{\partial x_2}h(x_1,x_2,x_3), T(x_2)^T \frac{\partial h(x_1,x_2,x_3)}{\partial x_3}) } \tag{1.11}$

　この時、それぞれの点のTangent Spaceの基底をそれぞれU,V（UV座標とかではなく任意の基底です）と考えます。それぞれの頂点には基底U,Vの位置微分 $\partial_u x_i,\partial_v x_i$ 、法線微分 $\partial_u n_i, \partial_v n_i$ を得られるとします。それぞれの意味はU、V方向にx_iを少しだけ動かした時の移動量と法線の変わり具合を示しており、実際のパストレで簡単に得られるとされています。

　次に各頂点をU,V空間上の座標(u,v)で表すこととします。 $(u_i,v_i)$ 上に存在する $x_i$ の座標というのは $\partial_u x_i,\partial_v x_i$ を用いて、以下のように表すことができます。また、その場所の法線も同様に表すことができます。 $u_i = 0, v_i = 0$ の時は頂点 $x_i$ の位置となります。

$\displaystyle{ x_i(u_i,v_i) = x_i + u_i(\partial_u x_i) + v_i(\partial_v x_i)\\ \\ n_i(u_i,v_i) = n_i + u_i(\partial_u n_i) + v_i(\partial_v n_i) } \tag{1.12}$

　以上の論議は頂点 $x_i$ をTangent Space上の座標(u,v)として表現しようということで、Tangent Space上でちょっとだけ動いたら（＝微分）がどうなるかを表すのに便利なのでこのようにしたわけです。ちなみに $\partial_u x_i$ などが得られることを前提としていましたが、実際の実装でも例が当たったジオメトリから求められるのでこの辺は問題ありません。

　では、 $x_1$ の微分部分についてみていきましょう。 $T(x_2)$ については特に微分には無関係なので置いておいて、ハーフベクトル部分の計算をしていきます。先ほどのパラメーター化で $x_1$ は $x_1(u_1,v_1)$ となりますので、ハーフベクトルの微分というのは(u,v)各座標での微分として分けることができます。

$\displaystyle{ \frac{\partial h(x_1,x_2,x_3)}{\partial x_1} = \frac{\partial h(x_1(u_1,v_1)) }{\partial x_1(u_1,v_1)} = (\frac{\partial h(u_1)}{\partial u_1},\frac{\partial h(v_1)}{\partial v_1}) } \tag{1.13}$

　ハーフベクトル $h(x_1, x_2, x_3)$ の計算は実際には

$\displaystyle{ (\frac{x_1 - x_2}{||x_1 - x_2||} + \frac{x_3 - x_2}{|| x_3 - x_2||} )/ ||\frac{x_1 - x_2}{||x_1 - x_2||} + \frac{x_3 - x_2}{|| x_3 - x_2||}|| } \tag{1.14}$

となりますので、ベクトル $z(t) / || z(t) ||$ を $t$ に関する微分公式

$\displaystyle{ \frac{\partial }{\partial t} \frac{z(t)}{||z(t)||} = \frac{1}{||z(t)||} \frac{\partial z(t)}{\partial t} - \frac{z(t)}{||z(t)||^3} \langle z(t),\frac{\partial z(t)}{\partial t} \rangle } \tag{1.15}$

より求めることができます。 $\partial h(u) / \partial u$ は $x_1(u)$ の位置が求められるため、この式を求めることができ、 $T(x_2)$ と併せると2×2の行列として表現することができます。 $T(x_2)$ のtangetnSpaceの基底を $(s,t)^T$ とすると、

$\displaystyle{ \frac{\partial c(x_1,x_2,x_3)}{\partial x_1} = \begin{pmatrix} \frac{h(u_1,v_1)}{\partial u_1} \cdot s & \frac{h(u_1,v_1)}{\partial v_1} \cdot s\\ \frac{h(u_1,v_1)}{\partial u_1} \cdot t & \frac{h(u_1,v_1)}{\partial v_1} \cdot t \end{pmatrix} } \tag{1.16}$

と書き下すことができます。この式は $x_3$ でも同様であり、この式によって $\nabla C$ の両端は計算することができます。

一方で $x_2$ に関する微分は $h$ の微分に加え更に、 $T$ の微分も入ってきます。まず、 $T$ の微分の前に $(u,v)$ に関する関数として $T(u_2,v_2)$ について考えていきます。これは単純に $x_2$ がそれぞれ微小に動いた時の法線 $n_2(u_2,v_2)$ から新たにTangent Spaceを作る関数として考えればよいわけです。[Jakob 2013]では直交座標の作り方としてグラム・シュミットの正規直交化法を採用しており、 $T(u_2,v_2)$ は

$\displaystyle{ T(u_2,v_2) = \begin{pmatrix} \partial_u x_2 - \langle \partial_u x_2, n_2(u_2,v_2) \rangle n_2(u_2,v_2) \\ \partial_v x_2 - \langle \partial_v x_2, n_2(u_2,v_2) \rangle n_2(u_2,v_2) \end{pmatrix} } \tag{1.17}$

となります。これについて、 $u_2,v_2$ について微分すると式(1.12)より

$\displaystyle{ \frac{\partial T(u_2,v_2)}{\partial u_2} = \begin{pmatrix} -\langle \partial_u x_2,\partial_u n_2 \rangle n_2 -\langle \partial_u x_2, n_2 \rangle \partial_u n_2 \\ -\langle \partial_u x_2,\partial_v n_2 \rangle n_2 -\langle \partial_u x_2, n_2 \rangle \partial_u n_2 \end{pmatrix} \\ \frac{\partial T(u_2,v_2)}{\partial v_2} = \begin{pmatrix} -\langle \partial_u x_2,\partial_v n_2 \rangle n_2 -\langle \partial_u x_2, n_2 \rangle \partial_v n_2 \\ -\langle \partial_v x_2,\partial_v n_2 \rangle n_2 -\langle \partial_v x_2, n_2 \rangle \partial_v n_2 \end{pmatrix} } \tag{1.18}$

というように求めることができます。これによって $x_2$ についても求めることができるというわけです。

以上のことから、頂点の $\partial_u x_i, \partial_v x_i, \partial_u n_i, \partial_v n_i$ を得ることができれば $\nabla C$ の計算をすることができます。ではこの値とはどうやって得るのかというと３角ジオメトリでは基底方向のベクトルがそのまま $\partial_u x_i, \partial_v x_i$ となり、頂点の位置をそれぞれ $\partial_u x_i, \partial_v x_i$ で微小にずらした頂点の法線から $\partial_u n_i, \partial_v n_i$ の値を得ることが可能です。（この辺は[Zeltner et al. 2020]の実装などを見た方が良いと思います）

[Jakob 2013]では付録で $\nabla C$ のCプログラムが載せられていまして、以下のような形になります。

struct Vertex
{
    Point p;           // Vertex position
    Vector dpdu, dpdv; // Tangent vectors
    Normal n;          // Normal vector
    Vector dndu, dndv; // Normal derivatives
    float eta;         // Relative index of refraction
    Matrix2x2 A, B, C; // Matrix blocks of ∇C in the row
    // associated with the current vertex
};

void computeDerivatives(Vertex *v)
{
    /* Compute relevant directions and a few useful projections */
    Vector wi = v[-1].p - v[0].p;
    Vector wo = v[1].p - v[0].p;
    float ili = 1 / wi.length();
    float ilo = 1 / wo.length();
    wi *= ili;
    wo *= ilo;
    Vector H = wi + v[0].eta * wo;
    float ilh = 1 / H.length();
    H *= ilh;
    float dot_H_n = dot(v[0].n, H),
          dot_H_dndu = dot(v[0].dndu, H),
          dot_H_dndv = dot(v[0].dndv, H),
          dot_u_n = dot(v[0].dpdu, v[0].n),
          dot_v_n = dot(v[0].dpdv, v[0].n);
    /* Local shading tangent frame */
    Vector s = v[0].dpdu - dot_u_n * v[0].n;
    Vector t = v[0].dpdv - dot_v_n * v[0].n;
    ilo *= v[0].eta * ilh;
    ili *= ilh;
    /* Derivatives of C with respect to x_{i-1} */
    Vector
        dH_du = (v[-1].dpdu - wi * dot(wi, v[-1].dpdu)) * ili,
        dH_dv = (v[-1].dpdv - wi * dot(wi, v[-1].dpdv)) * ili;
    dH_du -= H * dot(dH_du, H);
    dH_dv -= H * dot(dH_dv, H);
    v[0].A = Matrix2x2(
        dot(dH_du, s), dot(dH_dv, s),
        dot(dH_du, t), dot(dH_dv, t));
    /* Derivatives of C with respect to x_i */
    dH_du = -v[0].dpdu * (ili + ilo) + wi * (dot(wi, v[0].dpdu) * ili) + wo * (dot(wo, v[0].dpdu) * ilo);
    dH_dv = -v[0].dpdv * (ili + ilo) + wi * (dot(wi, v[0].dpdv) * ili) + wo * (dot(wo, v[0].dpdv) * ilo);
    dH_du -= H * dot(dH_du, H);
    dH_dv -= H * dot(dH_dv, H);
    v[0].B = Matrix2x2(
        dot(dH_du, s) - dot(v[0].dpdu, v[0].dndu) * dot_H_n - dot_u_n * dot_H_dndu,
        dot(dH_dv, s) - dot(v[0].dpdu, v[0].dndv) * dot_H_n - dot_u_n * dot_H_dndv,
        dot(dH_du, t) - dot(v[0].dpdv, v[0].dndu) * dot_H_n - dot_v_n * dot_H_dndu,
        dot(dH_dv, t) - dot(v[0].dpdv, v[0].dndv) * dot_H_n - dot_v_n * dot_H_dndv);
    /* Derivatives of C with respect to x_{i+1} */
    dH_du = (v[1].dpdu - wo * dot(wo, v[1].dpdu)) * ilo;
    dH_dv = (v[1].dpdv - wo * dot(wo, v[1].dpdv)) * ilo;
    dH_du -= H * dot(dH_du, H);
    dH_dv -= H * dot(dH_dv, H);
    v[0].C = Matrix2x2(
        dot(dH_du, s), dot(dH_dv, s),
        dot(dH_du, t), dot(dH_dv, t));
}

　まず、頂点のVertexの情報ですが普段使う「位置座標p」、「法線n」、「IOR eta]の他に各微分情報「位置の微分dpdu,dpdv」「法線の微分dndu,dndv」を持っているとしています。これらの情報はジオメトリから計算することができます。なお、ここでは $\nabla C$ の結果を入れるためのA,B,Cという行列を用意しています。

struct Vertex
{
    Point p;           // Vertex position
    Vector dpdu, dpdv; // Tangent vectors
    Normal n;          // Normal vector
    Vector dndu, dndv; // Normal derivatives
    float eta;         // Relative index of refraction
    Matrix2x2 A, B, C; // Matrix blocks of ∇C in the row
    // associated with the current vertex
};

　 $\nabla C$ の計算はcomputeDerivativesの方で行っています。vertexにはSpecular点をv[0]、その前後の頂点をv[-1],v[1]として持っており、これを入力として受け取っています。

　最初の部分では入射、出射、ハーフベクトルなどの計算をしており、wi,wo,Hとして保存しています。また、各長さはili,ilo,ilhとして保存しており、これを用いて各ベクトルは正規化されています。その後、後々に使う計算用に各ベクトルの内積を計算しています。

    /* Compute relevant directions and a few useful projections */
    Vector wi = v[-1].p - v[0].p;
    Vector wo = v[1].p - v[0].p;
    float ili = 1 / wi.length();
    float ilo = 1 / wo.length();
    wi *= ili;
    wo *= ilo;
    Vector H = wi + v[0].eta * wo;
    float ilh = 1 / H.length();
    H *= ilh;
    float dot_H_n = dot(v[0].n, H),
          dot_H_dndu = dot(v[0].dndu, H),
          dot_H_dndv = dot(v[0].dndv, H),
          dot_u_n = dot(v[0].dpdu, v[0].n),
          dot_v_n = dot(v[0].dpdv, v[0].n);

　次に行うのが $x_2$ のTangent Space $T(x_2)^T$ を計算しています。この時の正規直交基底の生成にはグラム・シュミットの正規直交化法を使用しており、それぞれs,tとして持っています。そのあとのilo,iliの計算はハーフベクトルの計算などに使用するために屈折率で補正を行っています。

    /* Local shading tangent frame */
    Vector s = v[0].dpdu - dot_u_n * v[0].n;
    Vector t = v[0].dpdv - dot_v_n * v[0].n;
    ilo *= v[0].eta * ilh;
    ili *= ilh;

　次に行うことは $x_1$ の微分部分でハーフベクトルの微分を計算しています。ここではまず最初にdH_du, dH_dvで式(1.15)の第一項部分を計算しています。その後、次の式で式(1.15)の第二項目について計算している形です。最終的に得られる結果は行列Aへと式(1.16)の計算結果を入れているわけです。

/* Derivatives of C with respect to x_{i-1} */
    Vector
        dH_du = (v[-1].dpdu - wi * dot(wi, v[-1].dpdu)) * ili,
        dH_dv = (v[-1].dpdv - wi * dot(wi, v[-1].dpdv)) * ili;
    dH_du -= H * dot(dH_du, H);
    dH_dv -= H * dot(dH_dv, H);
    v[0].A = Matrix2x2(
        dot(dH_du, s), dot(dH_dv, s),
        dot(dH_du, t), dot(dH_dv, t));

　そのあとに続くものはx_2の微分、つまりSpecular点の微分部分です。これは先ほどと同様ハーフベクトルの微分を計算していますが、最後の行列部分でさらにTangent Spaceの微分式(1.18)を計算している形で行列を求めているというわけです。

/* Derivatives of C with respect to x_i */
    dH_du = -v[0].dpdu * (ili + ilo) + wi * (dot(wi, v[0].dpdu) * ili) + wo * (dot(wo, v[0].dpdu) * ilo);
    dH_dv = -v[0].dpdv * (ili + ilo) + wi * (dot(wi, v[0].dpdv) * ili) + wo * (dot(wo, v[0].dpdv) * ilo);
    dH_du -= H * dot(dH_du, H);
    dH_dv -= H * dot(dH_dv, H);
    v[0].B = Matrix2x2(
        dot(dH_du, s) - dot(v[0].dpdu, v[0].dndu) * dot_H_n - dot_u_n * dot_H_dndu,
        dot(dH_dv, s) - dot(v[0].dpdu, v[0].dndv) * dot_H_n - dot_u_n * dot_H_dndv,
        dot(dH_du, t) - dot(v[0].dpdv, v[0].dndu) * dot_H_n - dot_v_n * dot_H_dndu,
        dot(dH_dv, t) - dot(v[0].dpdv, v[0].dndv) * dot_H_n - dot_v_n * dot_H_dndv);

　最後は終点 $x_3$ の計算でこれは $x_1$ と同様に行っています。

    /* Derivatives of C with respect to x_{i+1} */
    dH_du = (v[1].dpdu - wo * dot(wo, v[1].dpdu)) * ilo;
    dH_dv = (v[1].dpdv - wo * dot(wo, v[1].dpdv)) * ilo;
    dH_du -= H * dot(dH_du, H);
    dH_dv -= H * dot(dH_dv, H);
    v[0].C = Matrix2x2(
        dot(dH_du, s), dot(dH_dv, s),
        dot(dH_du, t), dot(dH_dv, t));

　以上で $\nabla C$ の計算をプログラムとして計算することができ、Manifold Walkを実装することができるというわけです。なお、多分ですがTangent Spaceの基底は任意であるため、重心座標系やUV座標系をTangent Spaceの基底として使用することも可能と思われます（いくつか実装を見たところそれぞれの実装で使いやすい物を使用している節があります）。　

Manifold Next Event Estimation

　Manifold ExplorationはSpecular面が存在するシーンで新たなパスを構築するのに便利でしたが、[Jakob Marschner et al. 2012]ではこの手法はMCMC上で使うことが目的でした。そこで、Manifold ExplorationをPathtracingへと応用したのがManifold Next Event Estimation(MNEE)[Hanika et al. 2015]になります。

　元論文では本当は[Jakob Marschner et al. 2012]のSpecular Manifoldをさらに一般化した[Kaplanyan et al. 2014],[Hanika et al. 2015b]のハーフベクトル条件を使った探索で論議しているのですが、多分Ideal reflection,refractionなら多分Manifold Explorationとして考えてもいいと思われます（この辺はちょっとまだ理解不足です）。

　以下のような床の上に雫があるようなシーンを考え、その内部に入っていったパスについて考えます。このシーンでは点光源 $x_c$ があり、雫の中に $x_b$ が今考えてるパスの点があるとします。

　通常のNEEでは点 $x_b$ から点 $x_c$ を直線的に繋げたようなパスを考えますが、今回の状況では中間に屈折鏡面が存在しているため、図上で点線で表されたパスというのはフェルマーの原理に反し、あり得ない経路となってしまいます。そのため、通常であればこのような状況ではNEEは全く使うことができません。

　[Hanika et al. 2015]はこれに対して、NEEで作った不可能なパス(Seed Path)からManifold Explorationによる探索で新たにフェルマーの原理を満たすようなパス(Admissible Path)を生成することで屈折境界面に対応したNEEを行うManifold NEEを提案しました。

　MNEEでは、まず $x_b$ と $x_c$ を直接NEEのように繋ぎ、その中間となるSpecular点 $x_3$ を得ます。このような直線的なパスはSeed Pathと言い、図上で点線で表される経路です。この時のSeed Pathを $Y$ と表現します。

　SpecularManifoldの方で論議した制約関数 $C$ にこのSeed Path $Y$ を入れるとその値というのはSpecular制限を逸脱しているため、

$\displaystyle{ 　 C(Y) \neq 0 } \tag{2.1}$

となります。一方でSpecular上ではどこかしらにはちゃんとフェルマーの原理を満たしたうえで $x_c$ と $x_b$ をつなぐことができるようなパスというのは存在するはずです。このパスはAdmissible Pathと言い、 $X$ と表記します。この時、 $X$ は当然以下のように $C$ の解として与えられます。

$\displaystyle{ 　 C(X) = 0 } \tag{2.2}$

これは逆を返せば、 $x_b,x_c$ における $C$ の解を求めることができれば、 $x_b,x_c$ をつなぐAdmissible Path $X$ を生成することが可能になると言えるわけです。

　ではどうやって解くのかというと、[Hanika et al. 2015]ではManifold Walkを使うことで解となるAdmissible Pathを探索します。今回、Manifold explorationの時とは状況が違い、 $x_b,x_c$ を固定したうえで、Specular上の点 $x_3$ を動かすような形でManifold Walkを行います。

　SeedPathの $x_3$ を初期値としてManifold Walkを行い、より $C$ の値が小さくなるような $x_3$ の移動量を求め、 $x_3$ を徐々に動かしていき $C$ が0になる位置 $x_3'$ を求めることでAdmissible Pathを求めます。

　イメージとしては $x_3$ に関する $C$ の多次元ニュートン法で解を徐々に求めていくという形です。

$\displaystyle{ 　 x_{i+1} = x_i - \frac{C(x_i)}{\nabla C(x_i)} } \tag{2.3}$

　Manifold WalkでAdmissible Pathさえ見つかれば、それによる寄与というのは簡単に計算でき（Ideal Specularにおいては）、アルゴリズムとしては以下のようになります。

　 $x_2~x_{n-1}$ はスペキュラー上の点であり、これらに対しManifold Walkをすることで新たに解として $x_2' ~ x_{n-1}'$ を取得します。この経路がAmissible Pathであり、このパスの寄与をそのまま計算するという形でMNEEのアルゴリズムが働きます。なお、Admissible Pathの確率密度はSeedPathの確率密度に等しいですので寄与の計算の際は $p(x_n)$ というSeedPathの確率密度を使用しています（詳しい話は後述）。

　残念ながらMNEEの直接的な実装はまだ見つけていないため、MNEEにおけるManifold Walkの具体的な実装法はよくわかっていませんが、[Zeltner et al. 2020]のManifold Walkと思われる実装を見ると恐らくManifold Explorationの時のManifold Walkとそこまで変わらないものと思われます。

　以上がMNEEの簡単な説明になります。MNEEは特にシンプルな形状のスペキュラー面では非常にきれいにサンプリングすることができ、以下の図のような中にガラス内部に物体があるようなシーンでは非常に効果的です。また、ガラスによるCausticsもうまく出すことができ、Specular面が強く出るシーンでは非常に強力な手法となっています。

MNEEとBDPTの比較 [Hanika et al. 2015] fig1 より引用

　MNEEの元論文[Hanika et al. 2015]ではglossyな物体に対するMNEEなどを考えており、非常に一般的な手法として発表しています。しかも、最近では先ほど述べたようにBlender3.2でShadowCausticsという形で実装されており、その実用性は非常に高いようです。

MNEEの問題点

　MNEEはPathTraceでCauticsを出す数少ない有効な手法でした。しかしながら、１つのSeed PathからAdmissible Pathは１つしか作れない、つまりSeed PathとAdmissible Pathは1対1の関係にあるという問題があります。

　これはなぜかというと、Admissible Pathの確率密度の計算のためです。今１つのSeed Path $\bf{Y}$ を用意したものとしましょう。本当であれば $x_b$ と $x_c$ を通るようなパス、つまりAdmissible Path $\bf{X}$ は雫の下部分を通っているものもあれば上部分から来たりするパスなどいくつもの経路を考えることができます。　Seed PathはこれらのAdmissible Path $\bf{X_i}$ からどれか一つを探索するわけなのですが、あるAdmissibleパス $\bf{X_k}$ を見つけた際にこの $\bf{X_k}$ のパスの確率密度 $P(\bf{X_k})$ はSeed Path $\bf{Y}$ に依存し、なおかつ他のAdmissible Pathを取る可能性もあったため

$\displaystyle{ 　P(\bf{X_k}) =\mathrm \int P(\bf{X_i} | \bf{Y}) P(\bf{Y}) d\bf{X} } \tag{1.9}$

と表されます。 $P(\bf{X_i | Y})$ については実際にやってみないと計算することが不可能であるため、この積分というのは計算することができません。

　MNEEではこの問題に対して、あるSeed Path $\bf{Y}$ に対してただ一つのAddmissible Path $X_Y$ のみを取るという条件を課すことで解決しています。このようにすることで $P(\bf{X_i | Y})$ は $P(\bf{X_Y | Y})$ のみ１となり、それ以外は０ということになり、

$\displaystyle{ 　P(\bf{X_Y}) =\mathrm \int P(\bf{X_i} | \bf{Y}) P(\bf{Y}) d\bf{X} = P(Y) } \tag{1.9}$

というようにSeed Pathの確率をそのまま使うことができます。実装上ではManifold Explorationの初期値に乱数を入れなければ固定のAddmissible Pathに収束するのでSeedPathをそのまま与えて探索しています。

　これの何が問題かというと、裏を返せばこれは複数個あるAddmissible Pathを１つ以外破棄しているということでもあります。そのため、本来ならいくつも経路があるのにそれらが一切取られないことによってCausticsにノイズが走ってしまう場合があります。これは経路の多さによって生じるため、より複雑な形状を持つような高周波Causticsでは特にMNEEは対応できない場合もあります。これがMNEEの大きな問題点として挙げられています[Zeltner et al. 2020]

Specular Manifold Sampling

　MNEEによってパストレでもCausticsを効率的に扱えるようになりましたが、以上のように高周波に限ってはまだまだ難しい問題でありました。しかしながら、比較的最近の2020年の論文[Zeltner et al. 2020] Specular Manifold Sampling for Rendering High-Frequency Caustics and Glintsにて高周波Causticsを効率的に扱えるSpecular Manifold Sampling(SMS)という手法が提案されました。SMSという手法はMNEEの確率密度問題を解決し、1つのSeedPathから複数のAddmissible Pathを扱えるようにした手法となっています。[Zeltner et al. 2020]ではunbiasな方法とbiasな方法の２つを述べています。

unbias SMS

　MNEEの問題とは先ほども述べたように、他の解がとられる確率というのが求められないため、以下の確率密度の積分を計算できないということでした。

$\displaystyle{ 　P(\bf{X_k}) =\mathrm \int P(\bf{X_i} | \bf{Y}) P(\bf{Y}) d\bf{X} } \tag{3.1}$

MNEEではこれを解決するためニュートン法における初期値を固定し、SeedPathとAdmissiblePathに１対１の対応を与えることで制限していました。

　一方でSMSは確率密度の逆数をうまい具合に計算することでどうにか以上の積分を数値計算する手法を見つけ、１つのSeedPathに対し複数のAdmissiblePathを生成することが可能しています。

　まずはAdmissiblePathを複数サンプルする方法について述べていきます。

　ニュートン法によって得られる解というのは与えた初期値に完全に依存しています。例えば、ある $x_2$ という初期値を与えるとその値から出る解というのは必ず１つの解 $x_2'$ だけになります。もし、他の解が得たいとなると初期値を $x_2$ ではなく、別の値 $y_2$ で与えて別途ニュートン法を行う他ありません。ですが、必ずしも $y_2$ から $x_2'$ 以外の解が出るわけではなく、同じ解 $x_2$ に収束する可能性もあり、その予測は非常に困難です。

　このような性質をよく表したのがニュートンフラクタルです。ニュートンフラクタルはある複素関数の解 $f(z) = 0$ について、複素平面上の点をニュートン法の初期値として与え、どの解に収束したかで色分けしたものです。ニュートンフラクタルは一般に複雑な形状をしており、初期値と解の複雑な関係性が見て取れると思います。

　手法の方に話を戻しまして、MNEEはニュートン法の初期値をDiffuse点 $x_1$ と光源点 $x_3$ を直接つないだ時の間の点 $2$ のみとしており、SeedPathから得られる解を１つだけに絞っていたわけです。一方でSMSでは初期値として与える $x_2$ に対してランダム性を与え、ニュートン法を行うことで他の解についても探索できるようにしています。

　 $x_2$ のサンプリング方法としてはDiffuse面のBSDFサンプリングの乱数を変えるなど色々考えられますがとにかく２つの一様乱数 $\bf{\xi} = \rm{(\xi_1,\xi_2)} \in ([0,1),[0,1))= \mathcal{U}$ によって生成されるものと考えます（[0,1]じゃないのは後の確率密度の条件を満たすため）。この際、 $x_2$ の各点はサンプル空間 $\mathcal{U} = (\xi_1,\xi_2)$ の点として表現することができます。

　こうして作った $x_2$ をニュートン法に掛けるとそれぞれ別々の解に収束して行きます。解 $k$ に収束する乱数点 $\bf{\xi}^{(k)}$ をとして、これの集合を $\mathcal{B_k} \subseteq \mathcal{U}$ と書きます。ニュートンフラクタルのように収束した解で色を付けると以下の図(d)のようになります。それぞれの色の領域が $\mathcal{B_k}$ となります。　

　こうすることで複数のAdmissiblePathをサンプルできるようにはなりましたが、問題はどうやってその確率密度を求めるかです。 $\bf{\xi}$ は一様乱数であり、 $\mathcal{U}$ 上のどの点も等しい確率で選ばれるため、ある解tex:kが選ばれる確率 $p_k$ というのは $\mathcal{B_k}$ の面積に等しいことになります

$\displaystyle{ 　p_k = \int_{\mathcal{U}} \mathbf{1}_{\mathcal{B_k}}(\bf{\xi}\mathrm{) d}\bf{\xi} } \tag{3.2}$

$\mathbf{1}_{\mathcal{B_k}}(\bf{\xi}\mathrm{)}$ は $\bf{\xi}$ の収束する解が $k$ であった時に１になりそれ以外は０となる関数です。この式も積分ではありますが、不偏推定量として以下のように求めることが可能です。

$\displaystyle{ 　\langle p_k \rangle= \frac{1}{N} \sum_{i=1}^{N} \mathbf{1}_{\mathcal{B_k}}(\bf{\xi_i}\mathrm{)} } \tag{3.3}$

　　これはつまり、いくつかサンプリングして採用する解 $k$ に収束した時に1、しなかったら0として総和を取り、平均すれば $p_k$ に近づくということです。一応、これで計算は不可能ではなくなったわけです。

　しかし、これには大きな問題があります。Pathtraceにおいては確率密度はそのままではなく、逆数 $1 / p_k$ で用いられます。ここで期待値の性質として逆数の期待値は元の期待値を逆数にしたものと一致しません $E(1/x) \neq 1/E(x)$ 。　すなわち

$\displaystyle{ 　\langle 1/p_k \rangle \neq 1 / \langle p_k \rangle } \tag{3.4}$

であり、(3.3)を求めたところで実際には使うことができません。ではどうするかというと、[Zeltner et al. 2020]は幾何級数展開を使うことで逆数の期待値 $\langle 1/p_k \rangle$ を求める手法を取りました。

　積分の逆数の不偏推定を求める問題は別のとこでも取り組まれており、[Booth 2007]から研究が始まりました。最近で[Qin et al. 2015]にてフォトンマッピングのファイナルギャザリングで使用する逆数の不偏推定量を求める方法を新たに開発していました。[Zeltner et al. 2020]ではこのアイディアを元に逆数の不偏推定量ついて求める手法を取っています。

　このアイディア自体はとても単純で $1 / p_k$ について、以下のように考えます。

$\displaystyle{ 　 \frac{1}{p_k} = \frac{1}{\int_{\mathcal{U}} \mathbf{1}_{\mathcal{B_k}}(\bf{\xi}\mathrm{) d}\bf{\xi}} = \frac{1}{1 - a} } \tag{3.5}$

ここでは $a$ は $a = 1 - \int_\mathcal{U} 1_{B_k}(\xi) d\xi$ であり、 $k$ 以外の解が選ばれる確率を意味します。この時 $a ＜ 1$ である（[0,1)の範囲なので最大でも１以下になる）ことから、この値を $a$ の幾何級数の総和としてみなすことができます。

$\displaystyle{ 　 \frac{1}{p_k} = \frac{1}{1 - a} = \sum_{i=0}^\infty a^i } \tag{3.6}$

　これより、逆数の不偏推定量 $\langle 1/p_k \rangle$ については以下のように求められます。この際、級数部分の各 $a$ は $j$ 回目にサンプリングした時に $k$ に収束しない確率の推定量 $\langle a_j \rangle$ という形でみなして表し、それぞれ独立なため各推定量は分けることができます。

$\displaystyle{ 　 \langle \frac{1}{p_k} \rangle = 1 + \langle a_1 \rangle + \langle a_1 \rangle \langle a_2 \rangle + \langle a_1 \rangle \langle a_2 \rangle \langle a_3 \rangle + \langle a_1 \rangle \langle a_2 \rangle \langle a_3 \rangle \langle a_4 \rangle + ... }$

$\displaystyle{ 　 \langle \frac{1}{p_k} \rangle = 1 + \sum_{i = 1}^{\infty} \prod_{j=1}^i \langle a_j \rangle } \tag{3.7}$

　[Zeltner et al. 2020]では、この式の推定量について、 $j$ 回目のManifold walkで $k$ 以外の解に収束した時 $\langle a_j \rangle$ の部分の値を１、解 $k$ に収束したときは $\langle a_j \rangle$ の部分の値を０として与えることで計算することができると述べています（理由についてはいまいち理解できてません）。こうすることでUnbiasな確率密度の逆数 $1/p_k$ を求めることができるというわけです。

　この式の良いところとして、無限級数として表現されていますが、どれか一つでも $k$ の解に収束するとそれ以降の項はすべて０になるため、計算を打ち切ることが可能というところです。

　以上の話をまとめ、Unbias SMSのアルゴリズムは以下のようになります。

Unbias Specular Manifold Smapling [Zeltner et al. 2020]より引用

　まず初めにランダムにサンプルしたスペキュラー上の点 $x_2$ を初期値としてmanifold walkを行い、解 $x_2^{(k)}$ を得られたとします(Line1~2)。その次にこの解 $x_2^{(k)}$ がとられる確率の逆数 $1 / p_k$ を求めていきます。Line3 ~ 9は式3.7の計算であり、別でサンプルしたスペキュラー上の点でmanifold walkを行い新たな解 $x_2'$ を取得します。この解 $x_2'$ が $x_2^{(k)}$ であった場合（判定は距離）はこの時点で計算を終了、Line10へと向かいパスの計算を行います。そうでなかった場合は $1 / p_k$ の値に+1して、同様の処理を繰り返していきます。

　以上がUnbias SMSのアルゴリズムです。こうすることでMNEEでは扱えなかった高周波Causticsを効率的に扱うことができるようになりました。[Zeltner et al. 2020]でMNEEとUnbias SMSの比較として以下のような図が出されていましたが、その差はかなり違うことが見て取れ、かなり強力な手法のように見えます。

5分間レンダリングでの各手法の比較 [Zeltner et al. 2020] fig14

　特に顕著なのが２番目の金属板のCusticsです。MNEEではほとんどCuasticsが見られませんがUnbiasedのものを見るとかなりCausticsが出ていることがわかります。これは特にこのCausticsが高周波（複数のAdmissiblePathが存在する)であるためで、大きな差があることが読み取れます。

　以上のようにSMSは高周波Causticsに対してかなり強い手法であるとわかります。

Bias SMS

　Unbias SMSは確率密度を求めるために複数の解を求めているのですが、これらは確率密度の計算以外には使われず破棄されています。Manifold walkはそこそこ重い処理であるため、せっかく解を求めたのに全くその寄与を得ないのは中々にもったいない気がします。

　せっかく得た解の寄与をどうにか計算しようと思うとMISが思いつきますが、他の解の確率密度を求めなくてはならず、複数の解を探索する必要がまた出てきます。結局のところMISでまとめて寄与を得ることは難しいです。

　[Zeltner et al. 2020]はこの問題に対して、Biasではありますがより実用的なSMSとしてBias SMSという手法を提案しています。

　M回サンプリングを行い、各解 $l = (1,2,...,L)$ を得たとします。この際、ある解 $l$ が得られた回数を[tex: n^l]と表記し、各解のパスの寄与を平均することで寄与 $Radiance$ を得ることとします。この時の式は

$\displaystyle{ 　 Radiance = \frac{1}{M} \sum_{l =1}^{L} n_l \frac{f(x_2^{(l)}) }{p(x_2^{(l)}) } } \tag{3.8}$

となります。この式の問題は各解の確率密度 $p(x_2^{(l)})$ を求めるのが難しいということです。ここで $p(x_2^{(l)})$ を以下のように近似することとします。

$\displaystyle{ 　 p(x_2^{(l)}) \approx \frac{n_l}{M} } \tag{3.9}$

単純にこれは確率の定義から考えられることで、これを(3.8)に代入すると

$\displaystyle{ 　 Radiance \approx \frac{1}{M} \sum_{l =1}^{L} n_l f(x_2^{(l)}) \frac{M}{n_l} = \sum_{l=1}^{L} f(x_2^{(l)}) } \tag{3.10}$

となります。

　式(3.10)は $M \rightarrow \infty$ であれば同値となりますが、中々にアバウトな近似となっていてある程度バイアスが生じることになります。[Zeltner et al. 2020]によると、このバイアスはエネルギーロスとして現れ、レンダリング結果がある程度暗くなってしまうことが述べられています。しかし、先ほどの図ではunbias、biasの結果がともに載っていますがそこまでバイアスが目立つことはなく、実用上あまり気にならない範囲ではあります。むしろ目立つノイズが消されるため、絵的にはより良い結果であるともいえます。

　Bias SMSのアルゴリズムは以下のように書くことができます。

アルゴリズムはとても簡単で、サンプル数Mを指定しその回数分Manifold Walkを行います。この際出てきた解を集め、それぞれの寄与を単純に加算したものを返すというだけです。

　Bias SMSによる最初のプールのレンダリング結果を見ると非常にきれいなCausticsが出ていることがわかります。

Biased SMS [Zeltner et al. 2020] Movie より引用

　SMSの説明は大まかにこんな感じになっています。ここでは省略しますが、元論文では他にもより効率的にManifold Walkができるようにパラメーターを変更する手法やGlint（凹凸が非常に激しい鏡面）のレンダリングなど様々な応用についても述ベています。

実装の資料

　MNEEの実装は今のところBlenderのリリースノートから飛んだ先のDeveloperのフォーラムに載っているものがありました（まだちょっと全部を見切れていないので確証はありませんが多分MNEEの実装であると思います）。

wiki.blender.org

https://developer.blender.org/rB1fb0247 　　ちなみに、2021年12月ぐらいにBlenderのShadow Causticsの実装に関するスレッドがあり、ここでMNEEについてやSMSの話題が出ていました（SMSを知ったのはここからでした）。この辺を探ってもいいかもしれないです。

developer.blender.org

　一方でSMSの実装については[Zeltner 2020]でGithub上でMitubaレンダラーの実装として公開されています。一部はMNEEと同様の処理を行うため、これよりMNEEの実装を見てもよいかと思います。

github.com

　[Zeltner et al. 2020]は他にも先行研究の手法などをまとめた動画を載せており、以上の記事で紹介した手法についてわかりやすくまとめられています。もし、興味があるのでしたら[Zeltner et al. 2020]の論文を一読してから他の論文をたどってみるとわかりやすいと思います。

　Specular Manifoldについては元論文の場所の実装リンクが途切れているので今のとこ実装を見つけていません。CausticsをレンダリングできるLuxCoreRendererがMLTで実装されているっぽいことに最近気づいたので、もしかしたら内部組み込まれているのかなと思ったりしています。

おわりに

　長い記事でしたがご拝読ありがとうございます。

　話を前々から聞いていて参加したかったレイトレ合宿が遂に開催されるということで、何かしら独自性のあるレンダラー作りたいなーとなんかしら探っていたところ先ほどのBlenderのShadow Causticsが発表されました。発表を見てみるとCausticsがちゃんと出てて、これ実装すれば結構良さそうと思い立ちMNEEを実装しようと色々情報を調べていきました。

　ですが調べてみるとMNEEは日本語情報が全くないし、理論がめちゃくちゃ難しく、しかも実装が見当たらないという壁に当たり、四苦八苦どうにか先行研究やBlenderのフォーラム漁ってなんとか調べた結果がこの記事で紹介した論文達です。

　それらを調べて大体こんな感じなのかなぁっとわかってきた（気がするので）全部まとめたろとやった結果がこの記事ですが、正直言って解説した内容がちゃんとあってるかが不安です。ただこれらに関する資料をまとめた記事とかはないと思うので、もし記事を見て手法に興味を持った人がこれを足掛かりにしてくれれば幸いです。

　ここではCausticsに関わる部分だけを抜き出して解説していきましたが、それぞれの論文はCaustics以外にも様々な応用を考えてあります。Manifold ExplorationではGlossyやVolumeの物体にも対応できるように考えられており、MNEEではGlossyの物体にも一般化して理論を組み立てています。興味があれば是非見てみてください（~~誰かやって解説してください~~）。

　ちなみにSSSのNEEに応用した論文もあるそうで（中身はちゃんと見てないです）、Manifold Explorationを使う手法って意外と多そうな雰囲気がある気がします。

disneyanimation.com

　レイトレ合宿までに実装が間に合う気がしない